DIY laserstuurmodule voor Arduino: 14 stappen (met afbeeldingen)

2024 Auteur: John Day | [email protected]. Laatst gewijzigd: 2024-01-30 11:18

In deze Instructable zal ik de constructie demonstreren van een laserstraalbesturingsmodule met twee assen en één spiegel met behulp van 3D-geprinte onderdelen en goedkope componenten van eBay.

Dit project heeft overeenkomsten met Arduino Laser Show met volledige XY-besturing en Arduino Laser Show met echte Galvos, maar ik geloof dat het de eerste is die een 3D-geprint ontwerp gebruikt met goedkope elektromagneten. Ik plaats alle ontwerpbestanden onder de GPLv3 zodat het ontwerp kan worden verbeterd en verbeterd.

Hoewel ik op dit moment alleen de module heb geassembleerd en een aantal zeer eenvoudige testcode heb geschreven, hoop ik dat ik het op een dag naar een hoger niveau kan tillen door de vector grafische code van mijn eerdere Instructable, Super Fast Analog Voltages van Arduino op te nemen.

Stap 1: Verzamel de niet-3D-geprinte onderdelen

De lasermontage bestaat uit de volgende onderdelen:

• 4 micro-magneten
• Een 1/2 inch spiegel
• Vier M3-schroeven

De specifieke solenoïden die ik gebruikte, werden op eBay gekocht voor $ 1,45 per stuk. De ronde spiegel werd gevonden in het gangpad bij HobbyLobby - een pakket van 25 kostte me minder dan $ 3 dollar. Je kunt ook spiegels vinden op eBay.

Je hebt ook een goedkope laserpointer nodig, nogmaals, van eBay. Een violette laser samen met een glow-in-the-dark vel vinyl is een uitstekende combinatie voor dit project!

Een setje helpende handen is niet nodig, maar is wel erg handig voor het vasthouden en positioneren van de laserpointer. Een grote bindclip kan worden gebruikt om de aan / uit-knop ingedrukt te houden.

Je hebt een Arduino nodig (ik gebruikte een Arduino Nano) en een manier om de elektromagneten aan te drijven. Zoals VajkF in de opmerkingen heeft aangegeven, zou je een kant-en-klare H-brug kunnen gebruiken, zoals die op basis van de L298 of de L9110. Deze zijn direct beschikbaar op eBay voor een paar dollar en kunnen ook worden gebruikt voor het aandrijven van motoren en robotica-projecten.

Omdat ik geen H-brug had, bouwde ik mijn eigen driver uit discrete componenten:

• Vier NPN bipolaire transistors (ik gebruikte een MPS3704)
• Vier weerstanden (ik gebruikte 1,2k ohm weerstand)
• Vier diodes (ik gebruikte een 1N4004)
• Een 9V batterij en batterijconnector

De elektronische componenten kwamen uit mijn lab, dus ik heb geen exacte kosten voor ze, maar tenzij je de onderdelen al hebt of ze kunt opruimen, is het waarschijnlijk voordeliger om een vooraf gebouwde H-brug te gebruiken. Desalniettemin zal ik de schema's leveren voor het bouwen van uw eigen.

Stap 2: 3D print de spiegelstuurmodule

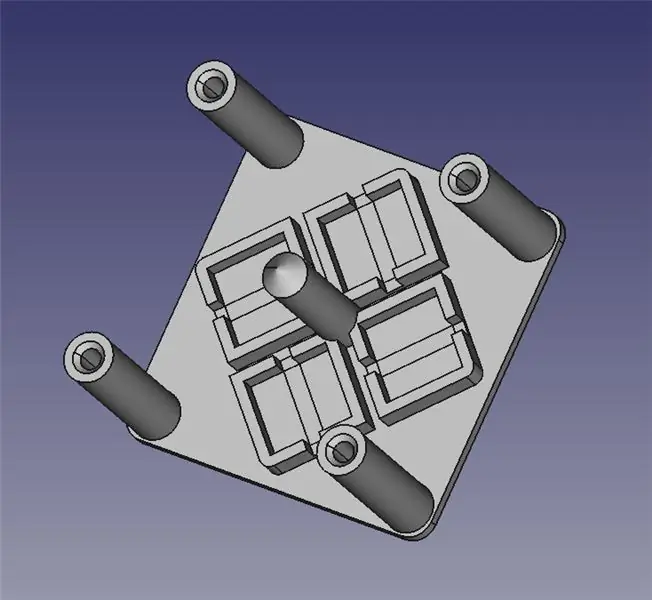
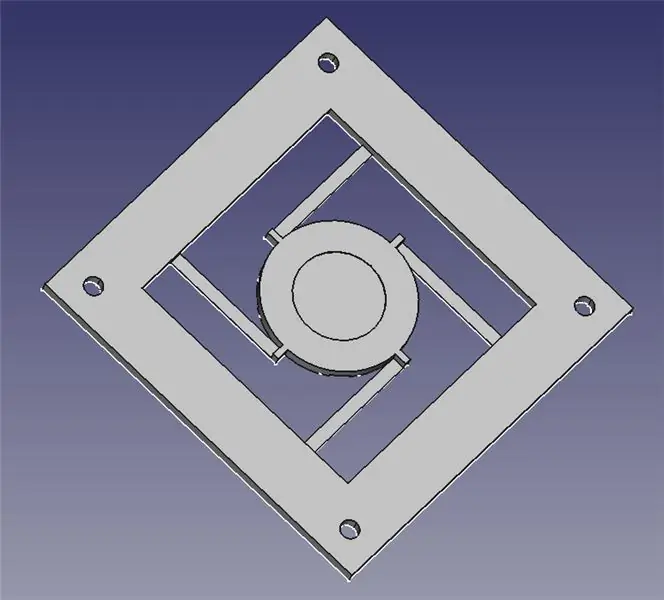
De laserstuurmodule bestaat uit twee 3D-geprinte delen: een basis voor het monteren van vier elektromagneten en een scharnierend platform voor de spiegel.

Ik heb de twee STL-bestanden voor u bijgevoegd voor 3D-printen, evenals FreeCAD-bestanden voor het geval u het ontwerp moet wijzigen. Alle inhoud valt onder de GPLv3, dus u bent vrij om uw verbeteringen aan te brengen en te delen!

Stap 3: Monteer de lasermodule

• Gebruik hete lijm om de vier elektromagneten op het onderste stuk te bevestigen.
• Gebruik hete lijm om de spiegel in het midden van het bovenste stuk te bevestigen.
• Plaats de metalen zuigers in de solenoïdes en plaats vervolgens het bovenste stuk op de palen (maar schroef het niet vast). Draai het bovenste stuk een beetje en gebruik een kleine schroevendraaier om elke zuiger op zijn plaats te tillen. De lip van de schijf moet in de groef op de zuiger schuiven. Wees voorzichtig, want de 3D-geprinte scharnieren zijn erg kwetsbaar. Met geduld en mogelijk een paar mislukte pogingen, zou u in staat moeten zijn om alle vier de zuigers te positioneren zonder te draaien of druk uit te oefenen op de scharnieren.
• Zodra alle zuigers zijn geplaatst, steekt u de M3-schroeven gedeeltelijk in, maar voordat u ze vastdraait, drukt u voorzichtig op elke zuiger en zorgt u ervoor dat de spiegel vrij kantelt. Als het niet vrij beweegt of blijft hangen, kan het nodig zijn om de bovenplaat te verwijderen, een of meer elektromagneten los te wrikken en deze onder een kleine hoek naar buiten weer te bevestigen (afstandhouders tussen de plaat en de middenstijl kunnen hierbij helpen).

Stap 4: Druk de laseraanwijzerhalsband af

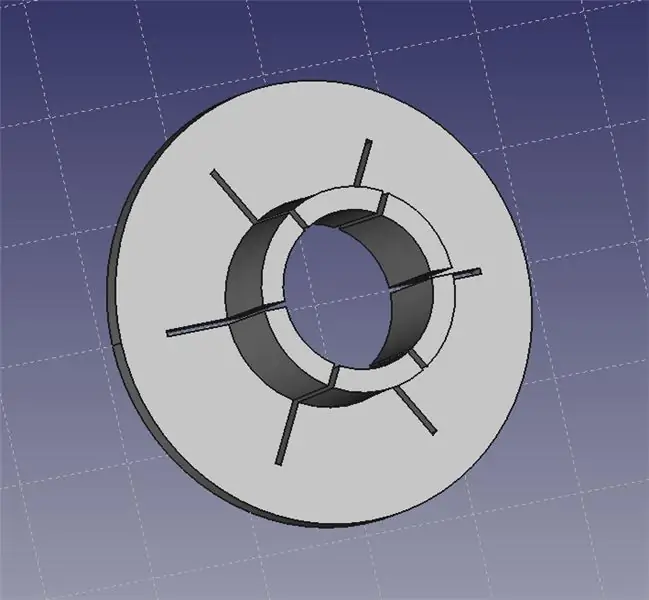
De laserpointer kraag past op de kop van de laserpointer. U kunt dan een set helpende handen gebruiken om de halsband vast te pakken en de laser precies op uw bank te positioneren.

Stap 5: Monteer het rijcircuit

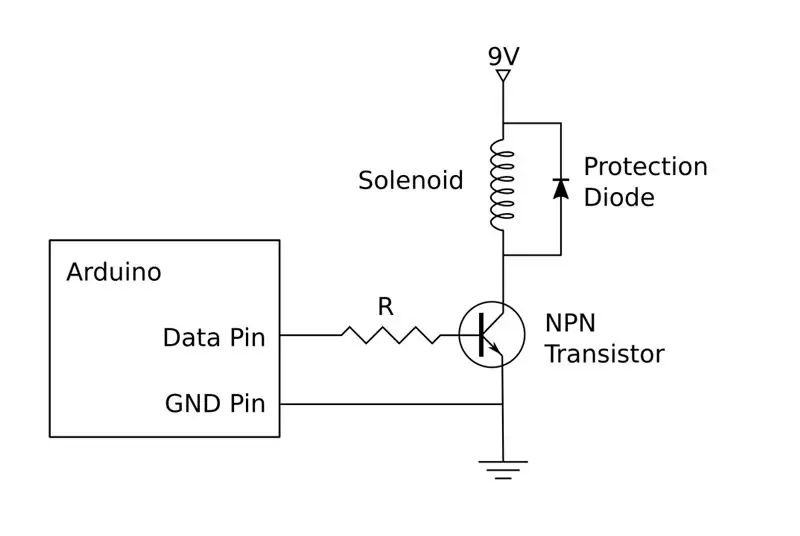
Het aandrijfcircuit wordt getoond in het schema. Zoals eerder vermeld, is mijn versie opgebouwd uit discrete componenten, maar je zou ook een gemakkelijk verkrijgbare H-brug kunnen gebruiken. Als u ervoor kiest om uw eigen circuit te bouwen, moet u vier exemplaren van dit circuit bouwen, één voor elk van de vier elektromagneten.

Elk circuit wordt aangesloten op een Arduino-pin, twee voor het besturen van de linker en rechter solenoïde, en twee voor de op en neer solenoïdes. Deze moeten worden aangesloten op PWM-compatibele pinnen, zoals:

• Pin 9: Solenoïde omhoog
• Pin 3: Solenoïde omlaag
• Pin 11: Linker solenoïde
• Pin 10: Rechter solenoïde

Een enkele 9V-batterij kan worden gebruikt voor het aansturen van alle vier de solenoïde-drivercircuits of u kunt een benchtop-voeding gebruiken. De Arduino werkt zonder USB-stroom en mag niet worden aangesloten op de positieve kant van de 9V-batterij. De negatieve kant van de batterij wordt echter gebruikt als grondreferentie en moet worden aangesloten op de GND-pin op de Arduino en op de emitterpinnen op de transistors.

Stap 6: Upload de voorbeeldcode

De voorbeeldcode is bijgewerkt met de volgende functies:

• Past de PWM-frequentie zodanig aan dat het mechanisme bijna stil is bij lage snelheden. Het zoemen in Motion Test 1 is helemaal weg!
• Voegt spanningsvergelijkingen toe op basis van het artikel van Schimpf om de niet-lineaire respons van de elektromagneten te "lineariseren".

Ik heb ook een implementatie van een Lorenz Attractor toegevoegd op basis van de code van deze blog.

De getrouwheid van de resultaten laat nogal wat te wensen over, maar ik ben er nog steeds mee bezig!:)

De volgende stappen illustreren enkele van de technieken die in de code worden gebruikt.

Stap 7: Het volume verlagen

In mijn Bewegingstest 1 hoor je een luid gezoem, met name tijdens op- en neergaande bewegingen. Het blijkt dat dit werd veroorzaakt doordat de standaard PWM-hakfrequentie van de Arduino binnen het hoorbare bereik lag. Het snel in- en uitschakelen van de spoelspanning zou ervoor zorgen dat ze op die frequentie gaan trillen, waardoor ze in kleine luidsprekertjes worden.

Om dit probleem op te lossen, heb ik de PWM-frequentie in de code verhoogd:

#define PWM_FREQ_31372Hz 0x01 // Stelt de PWM-frequentie in op 31372.55 Hz #define PWM_FREQ_3921Hz 0x02 // Stelt de PWM-frequentie in op 3921.16 Hz #define PWM_FREQ_980Hz 0x03 // Stelt de PWM-frequentie in op 31372.39 Hz void setPWMTimerB & 0b11111000) | frequentie; // Set timer1 (pins 9 & 10) frequentie TCCR2B = (TCCR2B & 0b11111000) | frequentie; // Stel timer2 (pins 3 & 11) frequentie in}

Het instellen van de Arduino PWM-frequentie is een handige truc om elektromagneten of motoren te stillen. Experimenteer met de verschillende frequentiekeuzes om te zien welke u de beste resultaten geeft. Hoewel het wat meer geavanceerde programmering omvat, is hier een goede bron over hoe de timers werken.

Stap 8: De spanningen afstemmen om vervorming te verminderen

Mijn eerste bewegingstests toonden aan dat er een significante vervorming was in de respons van de solenoïdes. In Bewegingstest 3 (linker figuur) werd wat een cirkelvormige spiraal moest zijn in plaats daarvan een rechthoekig web met gekartelde randen.

Het oplossen van dit probleem vergde wat wiskunde, maar ik kon een geweldig artikel op internet vinden dat me hielp het probleem goed genoeg te begrijpen om het in software op te lossen.

Wat volgt u door het proces dat ik heb doorlopen om het systeem af te stemmen en het uiterlijk van de resulterende sporen te verbeteren!

Stap 9: De software perfectioneren, met wiskunde

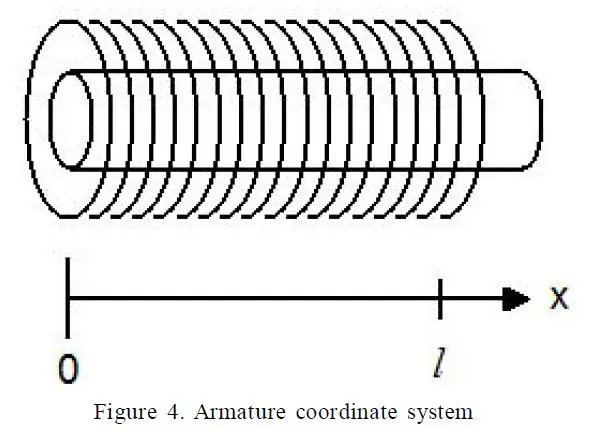
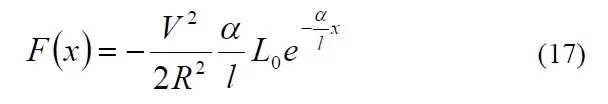
Het geheim van het afstemmen van het systeem bleek een uitstekend artikel te zijn met de titel "Een gedetailleerde verklaring van solenoïde kracht" door Paul H. Schimpf van de Eastern Washington University (link). In het bijzonder gaf vergelijking 17 me de solenoïdekracht in termen van verschillende termen.

De volgende termen waren gemakkelijk te meten:

• R - De weerstand van mijn solenoïde
• l - De lengte van de solenoïde
• x - De verplaatsing van de zuiger in de solenoïde
• V - De spanning over de solenoïde

Ik wist ook dat de kracht van de solenoïde de kracht van de 3D-geprinte veren op de dubbelassige spiegel moest compenseren. De kracht van een veer wordt bepaald door de wet van Hooke, die als volgt luidt:

F = -kx

Hoewel ik de waarde van k niet kende, wist ik in ieder geval dat de kracht die ik uit vergelijking 17 van Schimpf's paper haalde, gelijk moest zijn aan de kracht van de wet van Hooke.

De waarde van alfa (α) was een lastige. Hoewel vergelijkingen 13 en 14 lieten zien hoe deze waarden te berekenen uit het gebied van de solenoïde (A), het aantal windingen (N) en magnetische permeabiliteitswaarden (μ), wilde ik geen solenoïde uit elkaar halen om de aantal windingen, en ik wist ook niet uit welk materiaal de kern van mijn solenoïde was gemaakt.

Stap 10: Een goedkope componententester redt de dag

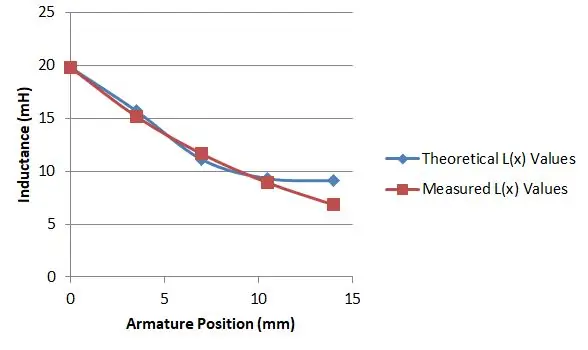
Het bleek echter dat vergelijking 15 en 16 me gaven wat ik nodig had. Ik had een goedkope M328-componententester die ik voor $ 10 van eBay had gekocht. Het was in staat om het te gebruiken om de inductantie van mijn solenoïde te meten en ik ontdekte dat door het anker op verschillende diepten in te drukken, ik verschillende inductiewaarden kreeg.

Door het te meten met het anker volledig ingestoken, kreeg ik de waarde van L (0).

De lengte van mijn solenoïde was 14 mm, dus ik heb de inductantie met het anker op vijf posities gemeten en dit gaf me verschillende waarden voor L(x):

• L(0,0) = 19,8 mH
• L(3.5) = 17.7 mH
• L(7.0) = 11,1 mH
• L(10,5) = 9,3 mH
• L(14) = 9,1 mH

Ik gebruikte vervolgens een spreadsheet om mijn waarden uit te zetten tegen de waarde van vergelijking 15 en 16, voor een bepaalde keuze van μr en varieerde mijn keuze totdat ik een goede overeenkomst vond. Dit gebeurde toen μr 2,9 was, zoals weergegeven in de grafiek.

Stap 11: Zoek de veerconstante K, los het probleem op

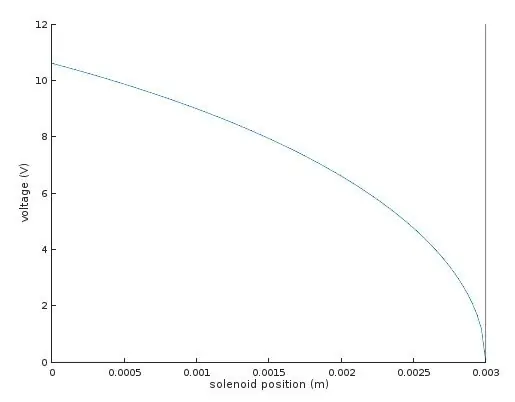
De enige overgebleven onbekende was K, de veerconstante. Ik heb dit gemeten door 9V toe te passen op een van de solenoïdes in mijn dubbelassige montage en de afstand te meten waarin de spiegel naar beneden werd getrokken. Met deze waarden kon ik de vergelijkingen voor K oplossen, die ik vond rond 10,41.

Ik had nu de waarden die ik nodig had om de trekkracht van de solenoïde op verschillende posities langs de slag te berekenen. Door F(x) gelijk te stellen aan de veerkracht uit de wet van Hooke, kan ik de vereiste spanning V oplossen.

De grafiek toont de spanning die nodig is om de solenoïde naar elke gewenste positie x te verplaatsen.

Aan de rechterkant, waar de spanning nul is en de positie 3 mm is, komt dit overeen met het neutrale rustpunt van de solenoïde wanneer de 3D-geprinte scharnieren volledig ontspannen zijn. Naar links bewegen op de grafiek komt overeen met het in de solenoïde trekken van het anker tegen de trekkracht van de 3D-geprinte scharnieren in - dit vereist aanvankelijk meer spanning, maar naarmate het anker dieper in de solenoïde komt, neemt de trekkracht toe en neemt de vereiste stuurspanning af.

Deze relatie is absoluut niet-lineair, maar met de vergelijkingen van Schimpf's paper kan ik mijn Arduino-code schrijven om de juiste spanningen uit te voeren, zodat de straalafbuiging lineair is:

float positionToVoltage(float x) {

// Herstelkracht uitgeoefend door scharnieren (wet van Hooke) op gewenste x. const float spring_F = -spring_K * (x - spring_X0); // Spanning zodanig dat de trekkracht van de solenoïde overeenkomt met de // herstelkracht van de scharnieren return sqrt(-2*R*R*(-spring_F)*solenoid_len/(a*L_0*exp(-a*x/solenoid_len)))); }

Dit leidt tot een veel meer cirkelvormige spiraal dan in mijn oorspronkelijke bewegingstest. Missie volbracht!

Stap 12: Vraag en antwoorden over het drivercircuit met discrete componenten

Waarom kan ik de solenoïde niet rechtstreeks op de Arduino aansluiten?

Het is een kwestie van hoeveel stroom de Arduino kan leveren zonder schade op te lopen. Dit is ongeveer 40mA per pin. Wetende dat de Arduino op 5V werkt, kunnen we de wet van Ohm gebruiken om de vereiste minimale weerstand van de belasting (in dit geval de solenoïde) te berekenen. 5 volt delen door 0,040 ampère geeft ons 125 ohm. Als de belasting een grotere weerstand heeft, kunnen we deze rechtstreeks op de Arduino aansluiten, anders niet. Een kleine solenoïde heeft meestal een weerstand van 50 ohm, dus we kunnen hem niet rechtstreeks vanuit de Arduino aansturen. Als we dat zouden doen, zou het 100 mA trekken, wat duidelijk te veel is.

Waarom gebruik je 9V voor de solenoïde, maar 5V voor de Arduino?

De Arduino draait op 5V, maar dit is iets te weinig voor een solenoïde. Door een transistor te gebruiken, kunnen we een spanning kiezen voor de solenoïde die onafhankelijk is van de 5V die voor de Arduino wordt gebruikt.

Hoe weet ik of een transistor geschikt is voor dit project?

Net als de Arduino is de belangrijkste vereiste dat de stroom die door de solenoïde vloeit, de maximale waarden voor de transistor (met name de collectorstroom) niet overschrijdt. We kunnen eenvoudig het worstcasescenario berekenen door de weerstand van de solenoïde te meten en vervolgens de voedingsspanning daardoor te delen. In het geval van een 9V-voedingsstroom voor de solenoïdes en een solenoïdeweerstand van 50 ohm, brengt het worstcasescenario ons op 180mA. De MPS3704 is bijvoorbeeld geschikt voor een maximale collectorstroom van 600 mA, wat ons een marge van ongeveer 3 geeft.

Hoe bepaal ik de minimale waarde van de weerstand die tussen de Arduino-uitgang en de basis van de transistor moet worden geplaatst?

De uitgang van de Arduino verbindt de basispoot van de bipolaire transistoren via een stroombegrenzende weerstand. Aangezien de Arduino op 5V werkt, kunnen we opnieuw de wet van Ohm gebruiken om de weerstand te berekenen die nodig is om de stroom onder de 40mA te beperken. Dat wil zeggen, deel 5 volt door 0,04 ampère om een waarde van minimaal 125 ohm te krijgen. Hogere weerstandswaarden zullen de stroom verlagen, waardoor we een nog grotere veiligheidsmarge hebben.

Is er een maximale waarde voor die weerstand die ik niet mag overschrijden?

Het blijkt, ja. Een transistor heeft een zogenaamde stroomversterking. Als de versterking bijvoorbeeld 100 is, betekent dit dat als we 1 mA in de basis plaatsen, er tot 100 mA door de belasting zal stromen die de transistor bestuurt. Als we 1,8 mA in de basis plaatsen, zal er tot 180 mA door de belasting stromen. Omdat we eerder hebben berekend dat bij 9V 180mA door de solenoïde stroomt, is een basisstroom van 1,8mA de "sweet spot", en minder en zal onze solenoïde niet volledig worden ingeschakeld.

We weten dat de Arduino 5V levert en we willen 1,8 mA stroom laten vloeien, dus gebruiken we de wet van Ohm (R=V/I) om de weerstand (R=V/I) te berekenen. 5V gedeeld door 1.8mA geeft een weerstand van 2777 ohm. Dus gezien de aannames die we hebben gemaakt, verwachten we dat de weerstand tussen 125 en 2777 moet liggen -- het kiezen van iets als 1000 ohm geeft ons hoe dan ook een redelijk goede veiligheidsmarge.

Stap 13: Analyse van huidige problemen en mogelijke oplossingen

Het huidige prototype toont potentieel, maar er blijven verschillende problemen:

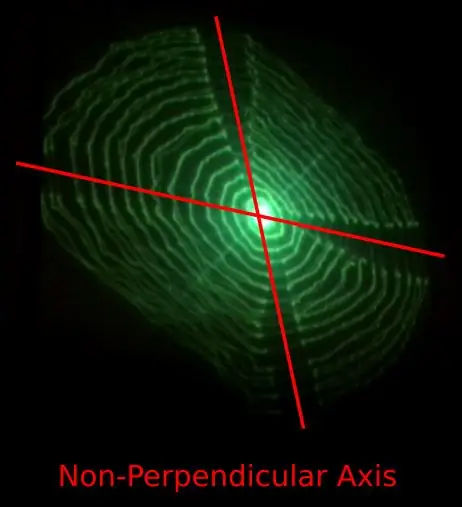
1. Beweging langs de X- en Y-as lijkt niet loodrecht te zijn.
2. Er is een sprong wanneer de spiegel van richting verandert.
3. De resolutie is vrij laag en er zijn zichtbare traptredepatronen.
4. Bij hogere bewegingssnelheden wordt het pad van de laser vervormd door trillingen en rinkelen.

Probleem 1) kan worden veroorzaakt door het ontwerp van de 3D-geprinte flexibele scharnieren die beweging langs één as naar de loodrechte as overbrengen.

Probleem 2) is te wijten aan speling in de koppeling tussen de aandrijfzuigers en het spiegelplatform, waardoor de spiegel schokt en springt bij overgangen tussen de X- en Y-as. Deze plotselinge beweging leidt tot een donkere X-vormige opening waar de laserpunt een snellere ongecontroleerde beweging maakt.

Probleem 3) treedt op omdat de standaard Arduino PWM slechts 255 niveaus heeft en nogal wat daarvan worden verspild vanwege de vorm van de spanningscurve. Dit zou aanzienlijk kunnen worden verbeterd door het gebruik van timer1, die 16-bits is en in staat zou zijn tot 65536 unieke waarden.

Probleem 4) treedt op omdat de spiegel en het glijdende anker (zuigers) van de solenoïde een aanzienlijke hoeveelheid bewegende massa vormen.

Aangezien problemen 1) en 2) verband houden met het mechanische ontwerp, is een mogelijkheid om de metalen zuigers te verwijderen en ze te vervangen door kleine zeldzame-aardmagneten die rechtstreeks op de kantelplaat zijn bevestigd. De solenoïden zouden een open spoel zijn die de magneten zou aantrekken of afstoten zonder fysiek contact te maken. Dit zou leiden tot een soepelere beweging en de mogelijkheid van schokken elimineren, terwijl de totale massa wordt verminderd.

Het verminderen van massa is de primaire oplossing voor probleem 4), maar eventuele resterende problemen kunnen direct in de software worden aangepakt door een motion control-profiel in software te implementeren om de spiegel op een gecontroleerde manier te versnellen en te vertragen. Dit wordt al op grote schaal gedaan in 3D-printerfirmware en vergelijkbare methoden kunnen hier ook werken. Hier zijn enkele bronnen met betrekking tot bewegingsbesturing zoals dit van toepassing is op 3D-printers:

• "Wiskunde van Motion Control-profielen", Chuck Lewin (link)
• "Jerk Controlled Motion Explained", (link)

Ik vermoed dat het toevoegen van een trapeziumvormig bewegingscontroleprofiel het mogelijk zou maken om de spiegel met veel hogere snelheden te laten rijden zonder rinkelende of trillingsartefacten.

Stap 14: Toekomstig werk en mogelijke toepassingen

Hoewel het ontwikkelen van oplossingen voor deze problemen veel werk zal vergen, heb ik goede hoop dat deze open-source bundelbesturingsmodule een betaalbaar alternatief kan worden voor op galvanometer gebaseerde projecten in toepassingen als:

• Een goedkope lasershow voor DJ's en VJ's.
• Een elektromechanische vectorweergave voor een vintage arcadespel zoals de Vectrex.
• Een doe-het-zelf SLA 3D-printer van het harstype die in de geest van de RepRap-beweging zijn eigen laserstuurmodule kan printen.
• Digitale panning of optische beeldstabilisatie voor camera's.

Tweede prijs in de Arduino-wedstrijd 2017