Tic Tac Toe op Arduino met AI (Minimax-algoritme) - Ajarnpa

2024 Auteur: John Day | [email protected]. Laatst gewijzigd: 2024-01-30 11:18

In deze Instructable laat ik je zien hoe je een Tic Tac Toe-spel kunt bouwen met een AI met behulp van een Arduino. Je kunt tegen de Arduino spelen of de Arduino tegen zichzelf zien spelen.

Ik gebruik een algoritme genaamd "minimax-algoritme", dat niet alleen kan worden gebruikt om een AI voor Tic Tac Toe te bouwen, maar ook voor een verscheidenheid aan andere spellen zoals Vier op een Rij, dammen of zelfs schaken. Games zoals schaken zijn erg complex en vereisen veel verfijndere versies van het algoritme. Voor ons Tic Tac Toe-spel kunnen we de eenvoudigste versie van het algoritme gebruiken, die niettemin behoorlijk indrukwekkend is. De AI is zelfs zo goed dat het onmogelijk is om de Arduino te verslaan!

Het spel is eenvoudig te bouwen. Je hebt maar een paar componenten nodig en de schets die ik heb geschreven. Ik heb ook een meer gedetailleerde uitleg van het algoritme toegevoegd, als je wilt begrijpen hoe het werkt.

Stap 1: Bouw en speel

Om het Tic Tac Toe-spel te bouwen, heb je de volgende componenten nodig:

• Een Arduino Uno
• 9 WS2812 RGB-leds
• 9 drukknoppen
• sommige draad en startkabels

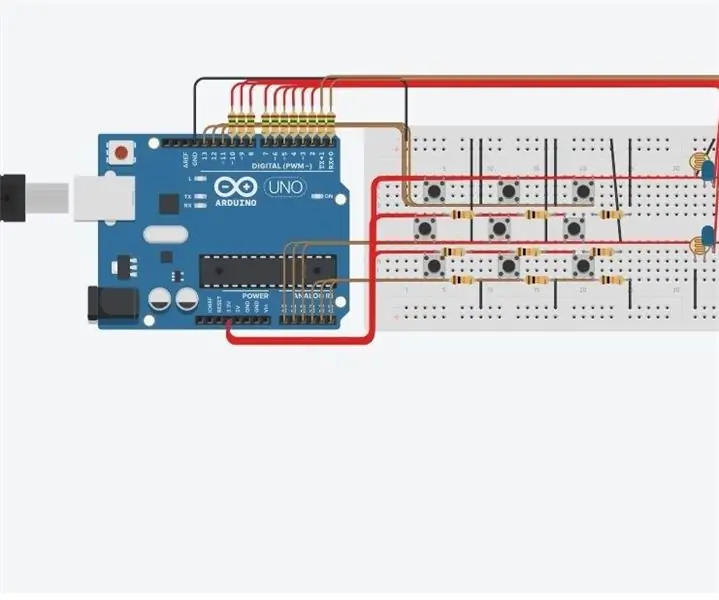
Sluit de componenten aan zoals weergegeven in de Fritzing-schets. Upload vervolgens de code naar uw Arduino.

Standaard neemt de Arduino de eerste beurt. Om het wat interessanter te maken, wordt de eerste zet willekeurig gekozen. Na de eerste zet gebruikt de Arduino het minimax-algoritme om de best mogelijke zet te bepalen. Je start een nieuw spel door de Arduino te resetten.

Je kunt de Arduino zien "denken" door de seriële monitor te openen. Voor elke mogelijke zet berekent het algoritme een rating die aangeeft of deze zet zal leiden tot een overwinning (waarde van 10) of een verlies (waarde van -10) voor de Arduino of een gelijkspel (waarde van 0).

Je kunt de Arduino ook tegen zichzelf zien spelen door de regel "#define DEMO_MODE" helemaal aan het begin van de schets te verwijderen. Als je de aangepaste schets uploadt, maakt de Arduino de eerste zet willekeurig en gebruikt vervolgens het minimax-algoritme om de beste zet voor elke speler in elke beurt te bepalen.

Merk op dat je niet kunt winnen tegen de Arduino. Elk spel eindigt in een gelijkspel of je verliest als je een fout maakt. Dit komt omdat het algoritme altijd de best mogelijke zet kiest. Zoals je wellicht weet, eindigt een spelletje boter en kaas altijd in een gelijkspel als beide spelers zich niet vergissen. In de demo-modus eindigt elk spel in een gelijkspel omdat, zoals we allemaal weten, computers nooit fouten maken;-)

Stap 2: Het Minimax-algoritme

Het algoritme bestaat uit twee componenten: een evaluatiefunctie en een zoekstrategie. De evaluatiefunctie is een functie die een numerieke waarde toekent aan bordposities. Als de positie een definitieve positie is (dwz een positie waar ofwel de blauwe speler of de rode speler heeft gewonnen of waar geen van beide spelers heeft gewonnen), is de evaluatiefunctie heel eenvoudig: laten we zeggen dat de Arduino blauw speelt en de menselijke speler rood speelt. Als de positie een winnende positie is voor blauw, kent de functie een waarde van 10 toe aan die positie; als het een winnende positie is voor rood, kent de functie een waarde van -10 toe aan de positie; en als de positie gelijkspel is, kent de functie een waarde van 0 toe.

Als de Arduino aan de beurt is, wil hij een zet kiezen die de waarde van de evaluatiefunctie maximaliseert, omdat het maximaliseren van de waarde betekent dat hij de voorkeur geeft aan een overwinning boven een gelijkspel (10 is groter dan 0) en een gelijkspel verkiest boven verliezen (0 is groter dan -10). Bij een analoog argument wil de tegenstander zo spelen dat ze de waarde van de evaluatiefunctie minimaliseert.

Voor een niet-eindpositie berekent het algoritme de waarde van de evaluatiefunctie door een recursieve zoekstrategie. Uitgaande van de huidige positie simuleert het afwisselend alle zetten die de blauwe en de rode speler kunnen doen. Dit kan worden gevisualiseerd als een boom, zoals in het diagram. Wanneer het een definitieve positie bereikt, begint het een stap terug te doen en draagt de waarde van de evaluatiefunctie van het lagere recursieniveau naar het hogere recursieniveau. Het wijst het maximum (als in de overeenkomstige recursiestap de blauwe speler aan de beurt is) of het minimum (als in de overeenkomstige recursiestap de beurt is aan de rode speler) van de waarden van de evaluatiefunctie toe van het lagere recursieniveau naar de positie op de hoger recursieniveau. Ten slotte, wanneer het algoritme klaar is met een stap terug te doen en weer op de huidige positie is aangekomen, neemt het die zet (of een van de zetten) die de maximale waarde voor de evaluatiefunctie heeft.

Dit klinkt misschien een beetje abstract, maar het is eigenlijk niet zo moeilijk. Beschouw de positie bovenaan het diagram. In de eerste recursiestap zijn er drie verschillende zetten die blauw kan doen. Blauw probeert de waarde van de evaluatiefunctie te maximaliseren. Voor elk van de zetten die blauw kan doen, zijn er twee zetten die rood kan doen. Rood probeert de waarde van de evaluatiefunctie te minimaliseren. Beschouw de zet waar blauw speelt in de rechterbovenhoek. Als rood in het middelste vak speelt, heeft rood gewonnen (-10). Als daarentegen rood in het middelste onderste vak speelt, wint blauw bij de volgende zet (10). Dus als blauw in de rechterbovenhoek speelt, speelt rood in het middelste vak, omdat dat de waarde van de evaluatiefunctie minimaliseert. Analoog, als blauw in het middelste onderste vak speelt, zal rood opnieuw spelen in het middelste vak, omdat dat de evaluatiefunctie minimaliseert. Als daarentegen blauw in het middelste vak speelt, maakt het niet uit welke zet rood neemt, blauw wint altijd (10). Omdat blauw de evaluatiefunctie wil maximaliseren, zal het in het middelste vak spelen, aangezien die positie resulteert in een grotere waarde van de evaluatiefunctie (10) dan de andere twee zetten (-10).

Stap 3: Problemen oplossen en verdere stappen

Als u op een knop drukt en een andere LED dan de LED die overeenkomt met de knop gaat branden, heeft u waarschijnlijk de draden op pinnen A0-A2 of 4-6 door elkaar gehaald, of u hebt de LED's in de verkeerde volgorde aangesloten.

Merk ook op dat het algoritme niet altijd een zet kiest die de Arduino zo snel mogelijk laat winnen. Ik heb zelfs wat tijd besteed aan het debuggen van het algoritme omdat de Arduino geen zet koos die een winnende zet zou zijn geweest. Het duurde even voordat ik me realiseerde dat het in plaats daarvan een zet had gekozen die garandeerde dat het een zet later zou winnen. Als je wilt, kun je proberen het algoritme aan te passen, zodat het altijd een winnende zet verkiest boven een latere overwinning.

Een mogelijke uitbreiding van dit project zou zijn om het algoritme te gebruiken om een AI te bouwen voor een 4x4 of zelfs een 5x5 Tic Tac Toe. Merk echter op dat het aantal posities dat het algoritme moet onderzoeken zeer snel groeit. U zult manieren moeten vinden om de evaluatiefunctie intelligenter te maken door waarden toe te kennen aan posities die niet definitief zijn, gebaseerd op de waarschijnlijkheid dat de positie goed of slecht is voor de speler in kwestie. U kunt ook proberen de zoektocht intelligenter te maken door de recursie vroegtijdig te stoppen als een zet minder waard blijkt te zijn om verder onderzocht te worden dan alternatieve zetten.

De Arduino is waarschijnlijk niet het beste platform voor dergelijke uitbreidingen vanwege het beperkte geheugen. Recursie laat de stapel groeien tijdens de uitvoering van het programma, en als de stapel te veel groeit, kan dit het programmageheugen beschadigen, wat kan leiden tot crashes of grillig gedrag. Ik koos de Arduino voor dit project vooral omdat ik wilde zien of het kon en voor educatieve doeleinden, niet omdat het de beste keuze is voor dit soort problemen.