Een geodetische koepel in Temcor-stijl maken in Autodesk Inventor: 8 stappen

2024 Auteur: John Day | [email protected]. Laatst gewijzigd: 2024-01-30 11:18

Deze zelfstudie laat u zien hoe u een koepel in Temcor-stijl kunt maken met slechts een klein beetje wiskunde.

De meeste informatie in deze tutorial is afgeleid van TaffGoch's reverse-engineering van de onderverdelingsmethode van het oude Amundsen-Scott South Pole Station, dus een grote dank aan hem!

Een groot voordeel van Temcor-domes is hun lage unieke stuttelling - het neemt rekenkundig toe met de frequentie, niet anders dan het reguliere triacontaëdrische geodetische raster van Duncan Stuart (methode 3*), maar het resultaat ziet er veel aangenamer uit.

Voor de eenvoud is de frequentie van de koepel die we maken 14, dus de akkoordfactoren kunnen worden vergeleken met het Temcor-model van TaffGoch.

De Inventor 2016.ipt is opgenomen aan het einde van de tutorial.

*UPDATE*

Ik beschreef methode 4 als Duncan Stuart's reguliere triacontaëdrische geodetische raster, maar dat is het niet. De methode is eigenlijk uitgevonden door Christopher Kitrick, die in zijn artikel uit 1985, "Geodesic Domes", de constructie ervan beschreef. Bovendien schetst hij in zijn paper uit 1990, "A Unified Approach to Class I, II & III Geodesic Domes", 8 andere methoden, een daarvan is Duncan Stuart's Method 3, de andere zijn eigen "Method 4", en verrassend genoeg genoeg, een methode die analoog is aan die van Temcor, die hij "Method aa" noemt (stap 7 laat zien hoe Temcor "Method aa" heeft gewijzigd). In een toekomstige instructable zal ik de constructie beschrijven van de methoden die in het laatste artikel worden beschreven.

Stap 1: Gebruikersparameters

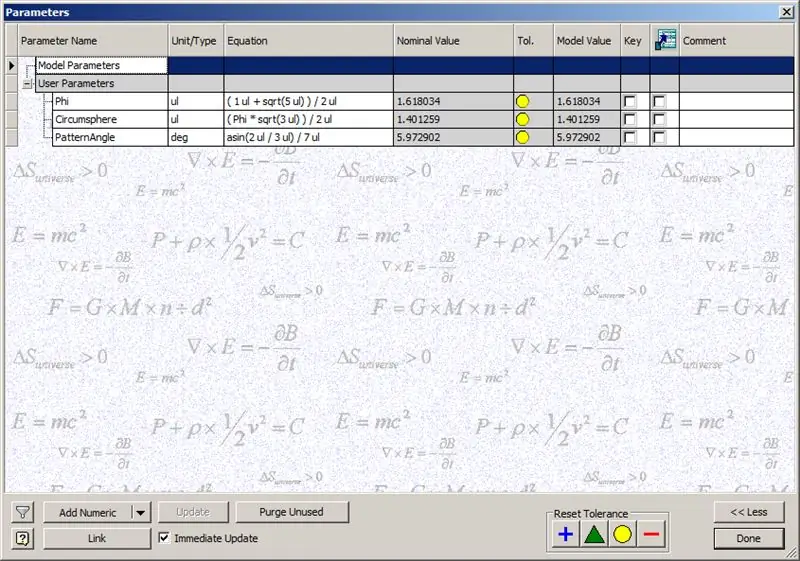
Voordat we beginnen met het bouwen van de koepel, voert u de getoonde parameters in:

Phi - De gulden snede. Gedefinieerd als ((1+√5/)2

Circumsphere - Dit is de circumsphere van een dodecaëder, gedefinieerd als ((Phi*√3)/2)

PatternAngle - Dit is de centrale hoek van een dodecaëder. Omdat de frequentie van onze koepel 14 is, delen we deze centrale hoek door de helft van de frequentie, in dit geval 7.

Stap 2: Een gouden rechthoek schetsen

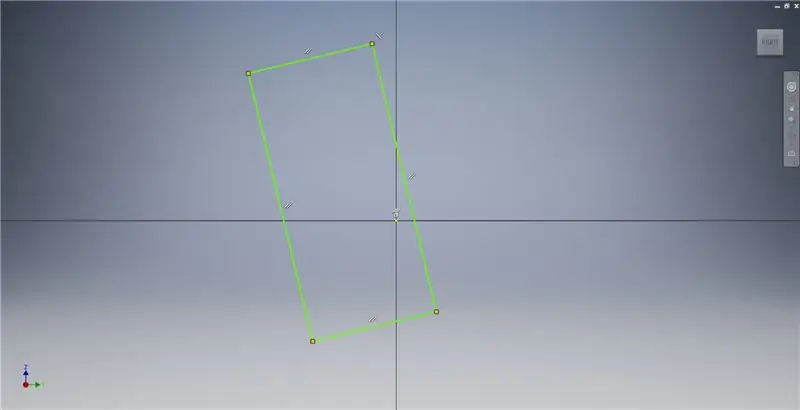
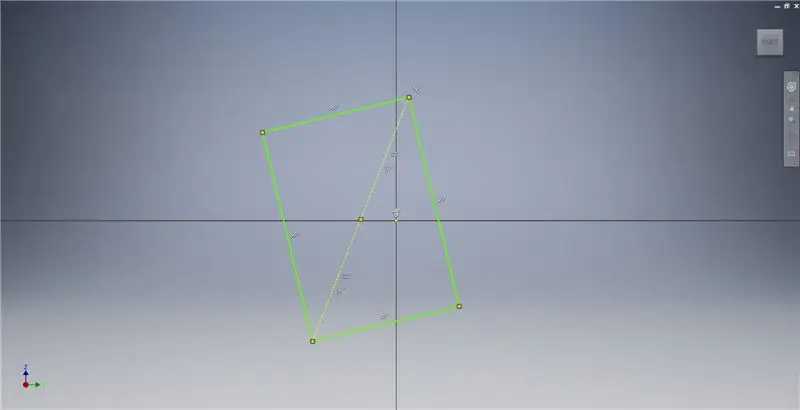
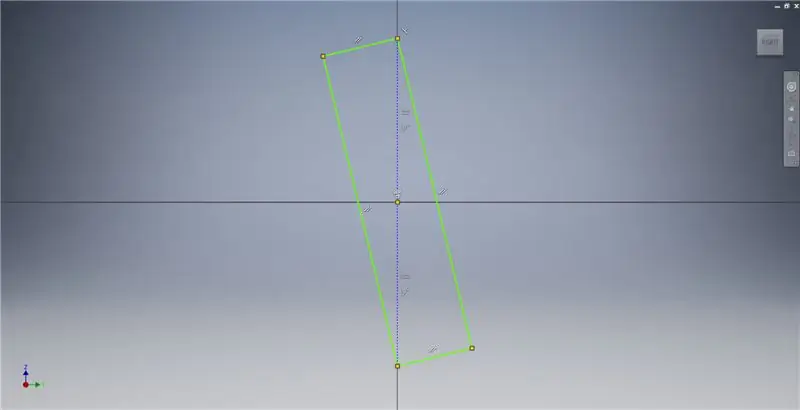
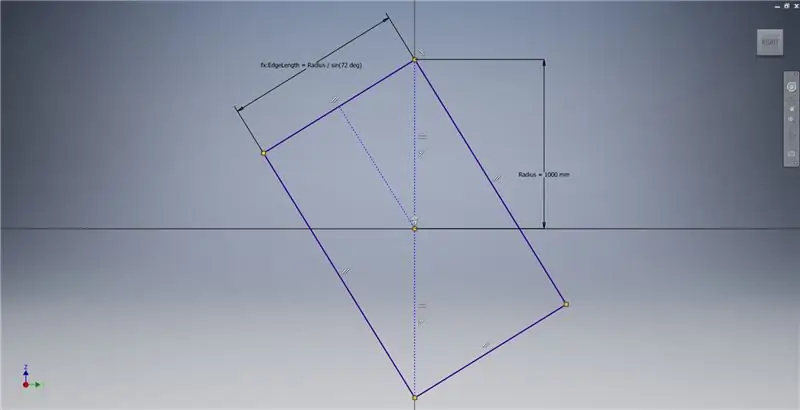
Start een schets op het YZ-vlak en maak vervolgens een driepunts rechthoek zoals weergegeven, verwijzend naar de afbeeldingsnotities voor aanvullende informatie over het maken van een gouden rechthoek.

Stap 3: Een gouden² rechthoek maken

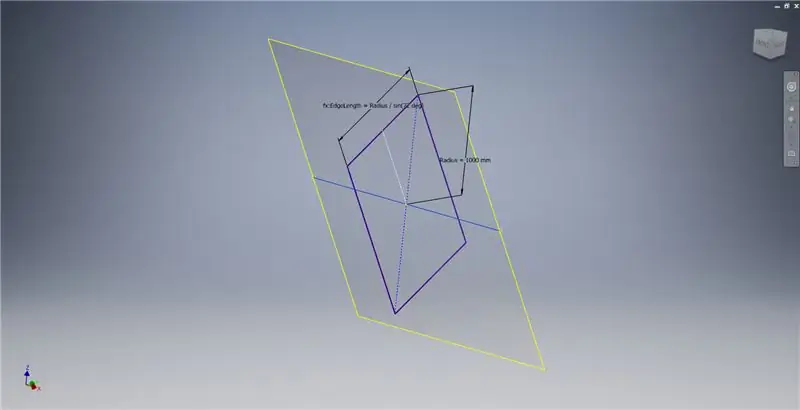
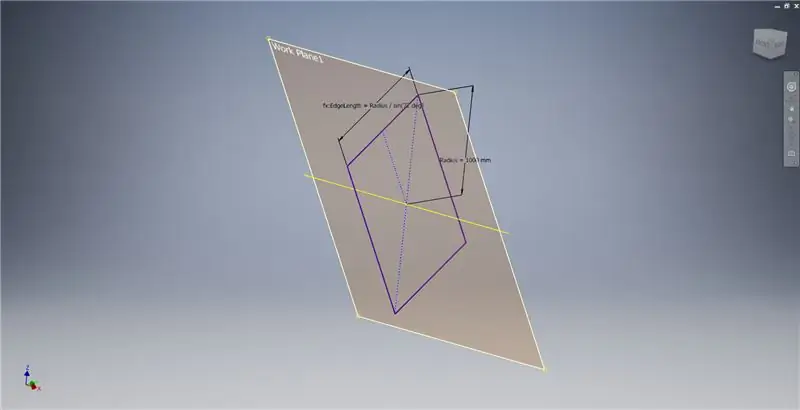
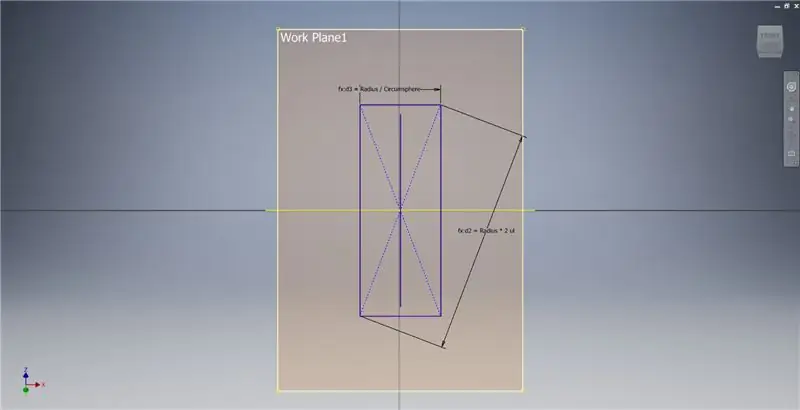
Maak een werkvlak met behulp van de X-as en de lijn die in de eerste afbeelding is gemarkeerd, en start vervolgens een nieuwe schets op dit werkvlak. Construeer een middelpuntrechthoek vanaf de oorsprong en bemat vervolgens de rechthoek zoals weergegeven in de derde afbeelding.

Stap 4: De 2v Triacon-driehoek maken

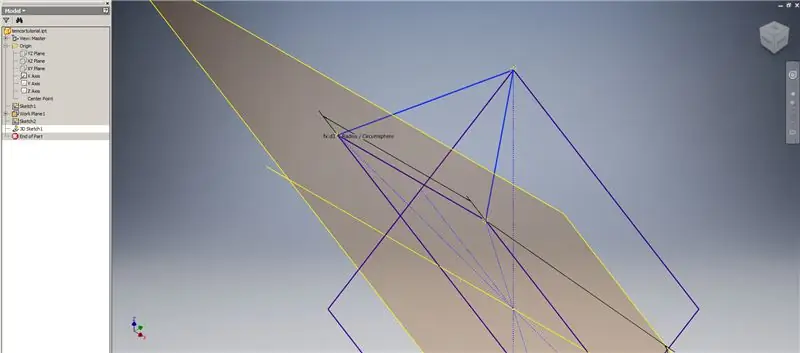
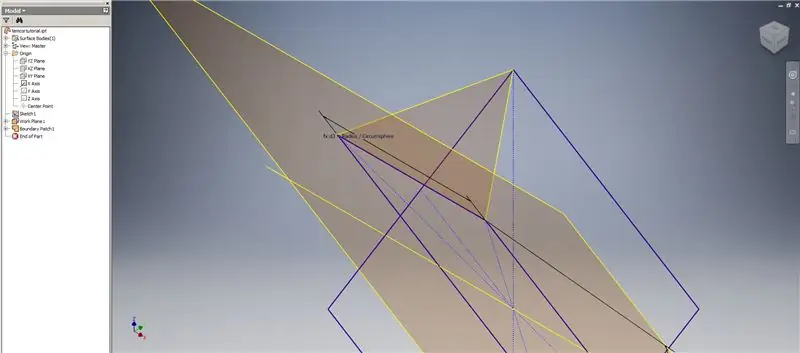
Nu we alle geometrie hebben die we nodig hebben, vormt u het grensvlak in de tweede afbeelding met de gewenste methode. Ik koos ervoor om een 3D-schets te maken, maar schetsen op een ander werkvlak zou net zo goed werken.

Stap 5: De snijvlakken maken

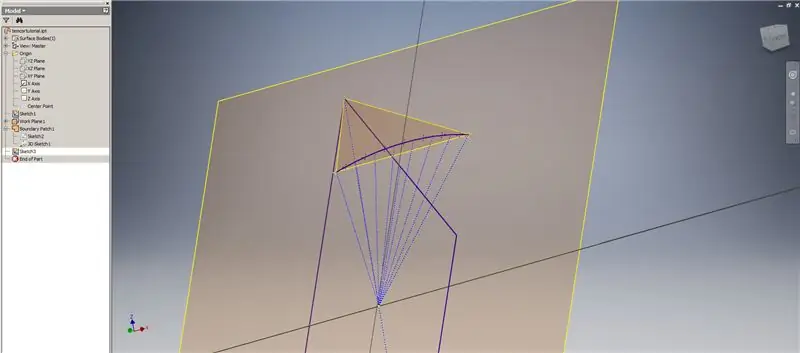
Start een nieuwe schets op het eerste werkvlak ("Work Plane 1") dat u hebt gemaakt, projecteer de hoeken van de Golden² Rectangle en verbind deze punten en de oorsprong om de centrale hoek van de 2v-triacontaëder te vormen. Deel het door de helft van de frequentie van de koepel, alsof u aan een methode 2-analyse begint. Plaats punten op de middelpunten van de akkoorden.

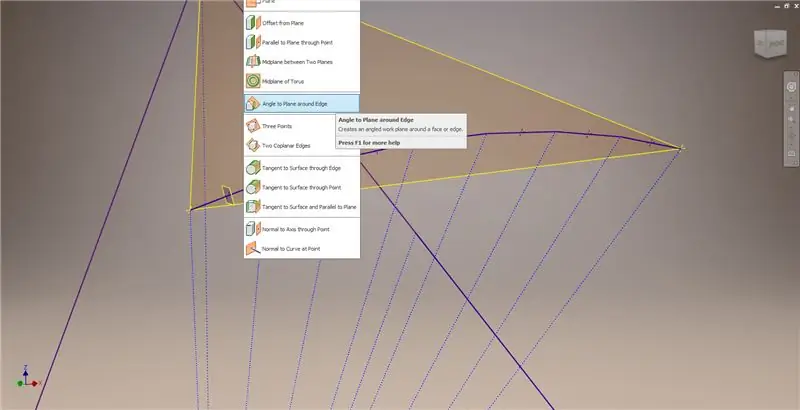
Verlaat de schets en maak vervolgens een vlak met behulp van een van de akkoorden en het middelpunt, zoals weergegeven in de tweede afbeelding. Maak vervolgens een ander werkvlak met behulp van "Angle to Plane around Edge". Selecteer Werkvlak 1 en een van de constructielijnen in de afbeelding rechts midden en linksonder. Accepteer de standaardhoek van 90 graden, anders zou de rest van de onderverdeling er niet goed uitzien. Herhaal het proces met de rest van de akkoorden en constructielijnen om het resultaat in de afbeelding rechtsonder te verkrijgen.

Stap 6: De snijpuntcurven maken en de onderverdeling vormen

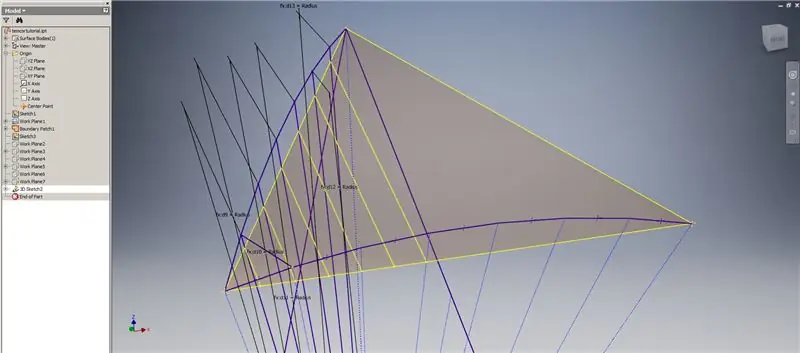
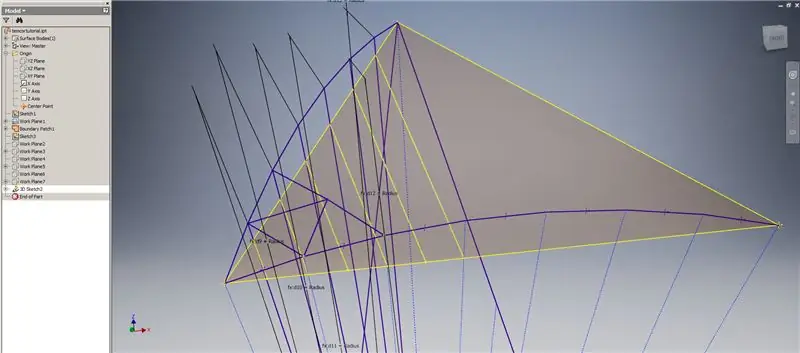
Start een 3D-schets en maak vervolgens snijpuntcurven met behulp van de werkvlakken die u zojuist hebt gemaakt en het grensvlak, zodat de lijnen worden gevormd die worden weergegeven in de bovenste afbeelding.

Trek lijnen die samenvallen met de eindpunten van de snijpuntcurven zoals weergegeven in afbeelding 2. Maak ze allemaal gelijk aan de straal van de koepel. Teken de akkoorden die de lijnen verbinden die op de snijpunten liggen. Verbind elke geometrie die dichtbij genoeg lijkt om een driehoek van de onderverdeling te vormen. Raadpleeg de volgende 10 afbeeldingen om te zien welke akkoorden over de werkvlakken van de kruising moeten worden gespiegeld - ze kunnen het beter uitleggen dan alleen woorden.

Stap 7: De koepel voltooien

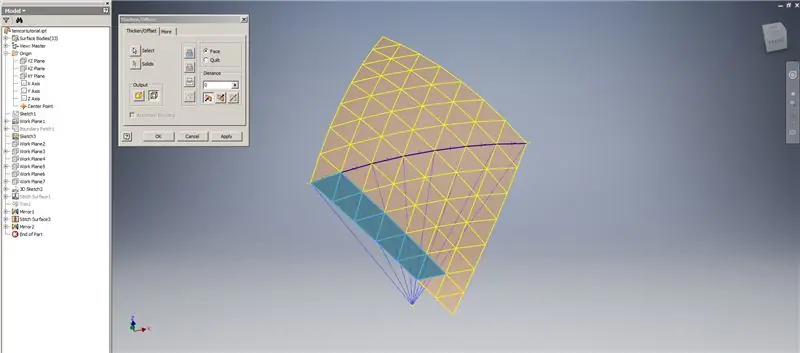
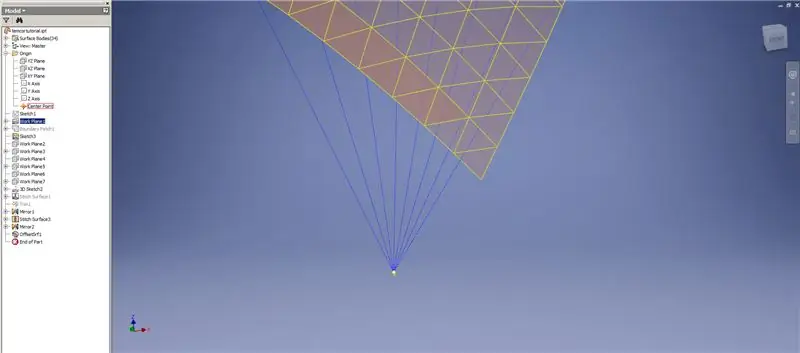
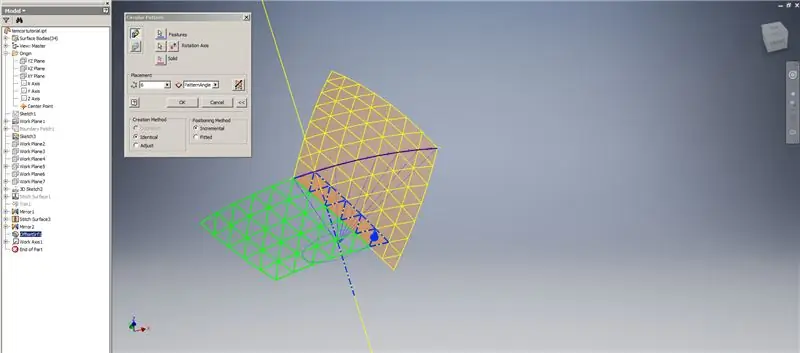
Maak een verdikking/offset van de onderste rijen, waarbij u de laatste twee rijen driehoeken weglaat. Patroon de nieuwe OffsetSrf 6 keer, of ((Frequency=14)/2)-1. Verberg de OffsetSrf, naai de patroonoppervlakken en spiegel vervolgens het genaaide oppervlak met het YZ-vlak. Maak werkvlakken die op de hoekpunten van de bovenste driehoek rusten, zoals weergegeven in Afbeelding 6. Knip de gestikte en gespiegelde oppervlakken bij met deze nieuwe werkvlakken en naai de resterende oppervlakken aan elkaar. Patroon dit laatste oppervlak over de Z-as, naai vervolgens deze laatste oppervlakken aan elkaar en u bent klaar!

Stap 8: Akkoorden controleren

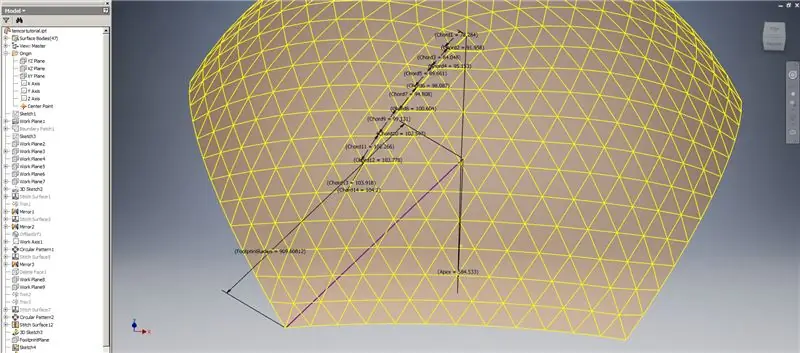
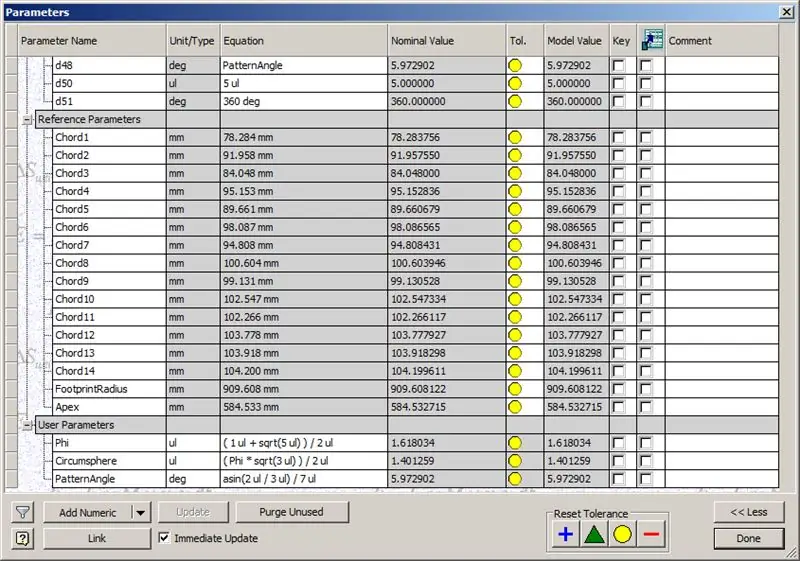
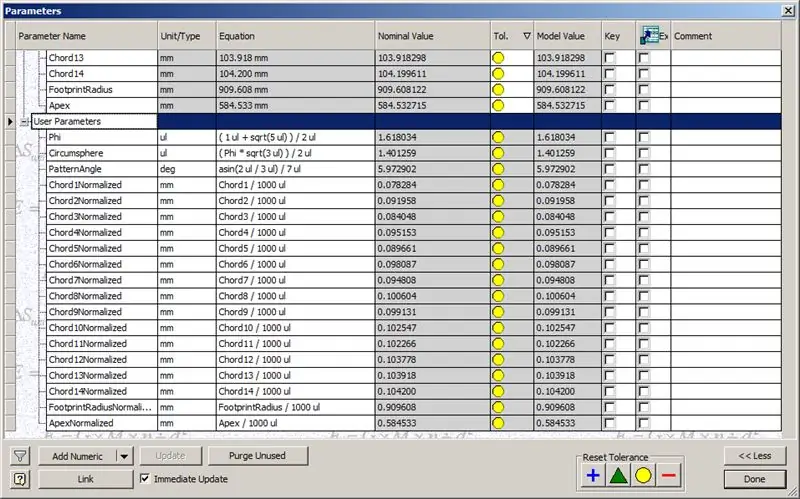
Onze koepel is dus klaar, maar laten we eens kijken of de cijfers overeenkomen met het model van TaffGoch:

Afgaand op de referentieparameters, lijkt het alsof ze een perfecte match zijn!

Als we de akkoordlengtes delen door 1000, kunnen we duidelijk een perfecte overeenkomst zien met de akkoordfactoren van het model van TaffGoch, evenals de voetafdrukradius en apexfactoren.