UStepper Robotarm 4: 5 stappen

2024 Auteur: John Day | [email protected]. Laatst gewijzigd: 2024-01-30 11:16

Dit is de 4e iteratie van mijn robotarm, die ik heb ontwikkeld als een applicatie voor onze uStepper stepper control board. Omdat de robot 3 stappenmotoren heeft en een servo voor bediening (in de basisconfiguratie), is hij niet beperkt tot de uStepper, maar kan hij worden gebruikt met elk stappenmotorbord.

Het ontwerp is gebaseerd op een industriële palletiseerrobot - en is relatief eenvoudig. Dat gezegd hebbende, heb ik talloze uren besteed aan het bedenken en optimaliseren van het ontwerp, zowel voor het gemak van de montage, maar ook voor het gemak van het printen van de onderdelen.

Ik deed het ontwerp met het gemak van afdrukken en eenvoud van montage in gedachten. Niet dat er geen manier is om die twee parameters te verbeteren, maar ik denk dat ik een lange weg heb afgelegd. Verder zou ik industriële robotica naar een niveau willen tillen waar hobbyisten het kunnen volgen door te laten zien dat het relatief eenvoudig kan worden gemaakt - ook de wiskunde om het te besturen!

Voel je vrij om een reactie achter te laten met constructieve feedback over zowel het ontwerp, maar vooral over hoe ik het voor iedereen toegankelijk maak (vooral de wiskunde).

Stap 1: Benodigde onderdelen, 3D-printen en monteren

Eigenlijk staat alles wat je moet weten in de montagehandleiding. Er is een gedetailleerde stuklijst met zowel gekochte als afgedrukte onderdelen en een gedetailleerde montage-instructie.

3D-printen gebeurt op een redelijke kwaliteit 3D-printer (FDM) met een laaghoogte van 0,2 mm en 30% vulling. U kunt de nieuwste versie van onderdelen en instructies hier vinden:

Stap 2: Kinematica

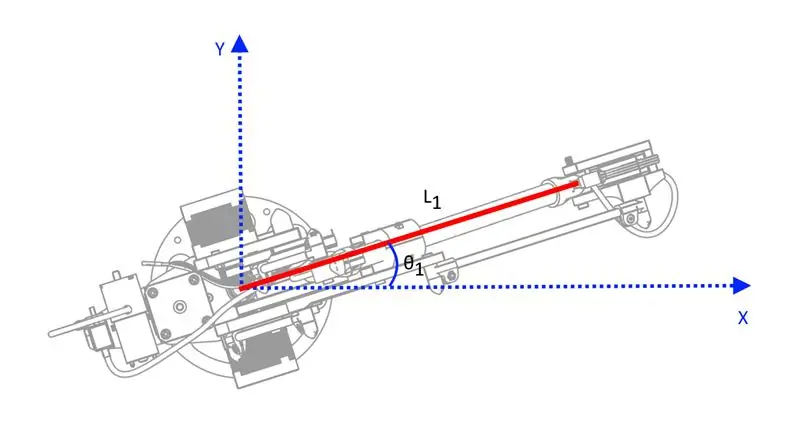
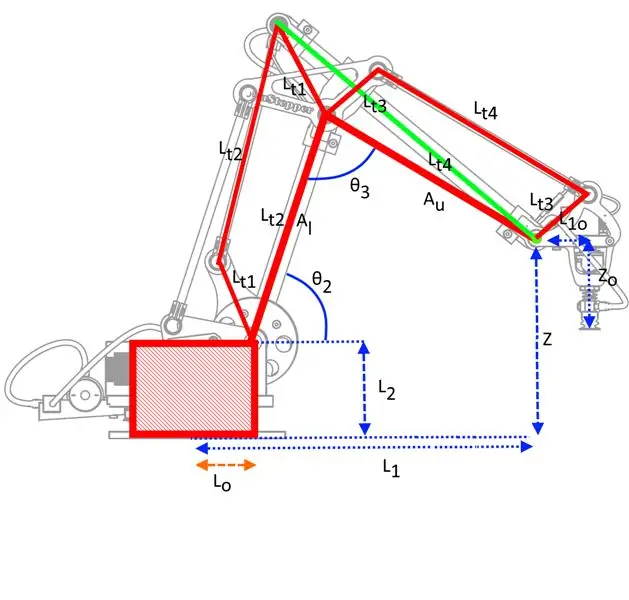
Om de arm op een voorzienbare manier te laten bewegen, moet je wiskunde doen: ik heb op veel plaatsen gezocht naar een relatief eenvoudige beschrijving van de kinematica die verband houdt met dit type robot, maar ik heb er geen gevonden waarvan ik denk dat die erop stond een niveau waarop de meeste mensen het konden begrijpen. Ik heb mijn eigen versie van de kinematica gemaakt die uitsluitend is gebaseerd op trigonometrie en niet op de matrixtransformaties die behoorlijk eng kunnen lijken als je nog nooit aan dat soort dingen hebt gewerkt - ze zijn echter vrij eenvoudig voor deze specifieke robot omdat het slechts 3 DOF is.

Niettemin denk ik dat mijn benadering in het bijgevoegde document op een relatief gemakkelijk te begrijpen manier is geschreven. Maar kijk eens of je er wat aan hebt!

Stap 3: Coderen van de kinematica

De kinematica kan moeilijk te begrijpen zijn, zelfs met de berekeningen die ik in de eerste heb gegeven. Dus hier is allereerst een Octave-implementatie - Octave is een gratis tool met veel van dezelfde functies als in Matlab.

L10 = 40;Zo = -70; L_2 = 73,0; Au = 188,0; Al = 182,0; Lo = 47,0; UPPERARMLEN = Au; LOWERARMLEN = Al; XOFFSET = Lo; ZOFFSET = L_2; AZOFFSET = Zo; AXOFFSET = L1o; disp('Code-implementatie') disp('Invoerhoeken:') rot = deg2rad(30); rechts = deg2rad(142.5); links = deg2rad(50); rad2deg(rot) rad2deg(rechts) rad2deg(links) T1 = rot;#base T2 = rechts;#schouder T3 = links;#elleboog #FW kinematica om XYZ vanuit hoeken te krijgen: disp('Berekend X, Y, Z:') z = ZOFFSET + sin(rechts)*LOWERARMLEN - cos(links - (pi/2 - rechts))*UPPERARMLEN + AZOFFSET k1 = sin(links - (pi/2 - rechts))*UPPERARMLEN + cos(rechts)* LOWERARMLEN + XOFFSET + AXOFFSET; x = cos(rot)*k1 y = sin(rot)*k1 ##inverse kinematica om hoeken uit XYZ te krijgen: rot = atan2(y, x); x = x - cos(rot)*AXOFFSET; y = y - sin(rot)*AXOFFSET; z = z - AZOFFSET-ZOFFSET; L1 = sqrt(x*x + y*y) - XOFFSET; L2 = sqrt((L1)*(L1) + (z)*(z)); a = (z)/L2; b = (L2*L2 + LOWERARMLEN*LOWERARMLEN - UPPERARMLEN*UPPERARMLEN)/(2*L2*LOWERARMLEN); c = (ONDERSTE ARMEN*ONDERSTE ARMEN + BOVENSTE ARMLEN*UPPERARMLEN - L2*L2)/(2*LOWERARMLEN*UPPERARMLEN); rechts = (atan2(a, sqrt(1-a*a)) + atan2(sqrt(1-b*b), b)); links = atan2(sqrt(1-c*c), c); ##output berekende hoeken disp('Output hoeken:') rot = rad2deg(rot) rechts = rad2deg(rechts) links = rad2deg(links)

Met het bovenstaande script heb je in principe de implementatieklare code voor voorwaartse en achterwaartse kinematica.

Forward Kinematics die je gebruikt om te berekenen waar je uitkomt met een bepaalde set motorhoeken. Inverse kinematica zal dan (het omgekeerde doen) berekenen welke motorhoeken je nodig hebt om op een gewenste x, y, z-positie te komen. Er moeten dan beperkingen op de motorische beweging worden ingevoerd, zoals b.v. roterende basis kan alleen gaan van 0 tot 359 graden. Zo zorg je ervoor dat je niet op posities komt die niet haalbaar zijn.

Stap 4: Het ding runnen

We zijn er nog niet helemaal met de implementatie van de kinematicabibliotheek, dus die kan ik nog niet geven. Maar ik kan je een video laten zien van hoe het werkt. Het is vrij stabiel en soepel door het gebruik van lagers en riemaandrijving, naast een redelijke kwaliteit van aandrijvingen die hier de uStepper S-borden zijn.

Stap 5: Extra eindeffectoren

Ik heb 3 extra eindeffectors ontworpen. De ene is gewoon een horizontale grijper, de andere past op een gewoon Europees bier- of frisdrankblikje en tot slot is er een vacuümgrijpersysteem waarmee je een vacuümbeker, pomp en klep kunt plaatsen.

Alles zal hier beschikbaar zijn of zijn (3D STL-bestanden en instructies):