Waarheidstabellen oplossen: 10 stappen

2024 Auteur: John Day | [email protected]. Laatst gewijzigd: 2024-01-30 11:15

Een waarheidstabel is een manier om alle uitkomsten van een probleem te visualiseren. Deze instructieset is gemaakt voor mensen die beginnen met discrete wiskunde. We zullen vandaag oefenen met een voorbeeldprobleem dat specifiek is voor deze instructies. Je hebt wat kladpapier en een potlood nodig om de tafel te visualiseren. Dit probleem duurt ongeveer 5 minuten voor mensen met voorkennis over het onderwerp en ongeveer 10 minuten voor beginners.

Voor deze instructieset zullen we ons concentreren op het probleem ~p Λ q. We gebruiken dit om enkele symbolen te introduceren die nodig zijn om waarheidstabellen te interpreteren.

Stap 1: Waarheidstabellen begrijpen

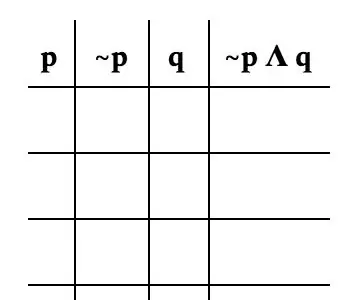
Een waarheidstabel is een manier om alle mogelijkheden van een probleem te visualiseren. Het kennen van waarheidstabellen is een basisbehoefte voor discrete wiskunde. Hier vinden we alle uitkomsten voor de eenvoudige vergelijking van ~p Λ q.

Stap 2: De symbolen kennen

De eerste stap naar de waarheidstafel is het begrijpen van de tekens. De "~" in dit specifieke probleem staat voor ontkenning. De "p" en "q" zijn beide variabelen. De "Λ" is gelijk aan "en". Deze vergelijking wordt gelezen als "niet p en q", wat betekent dat de vergelijking waar is als p niet waar is en q waar is.

Stap 3: De tabel opmaken

Nu om de eigenlijke tafel te vormen. Het is belangrijk om het probleem per variabele op te splitsen. Voor dit probleem zullen we het als volgt opsplitsen: p, ~p, q en ~p Λ q. De afbeelding is een goed voorbeeld van hoe uw tafel eruit moet zien.

Stap 4: Waar en niet waar toewijzen

Aangezien er slechts twee variabelen zijn, zijn er slechts vier mogelijkheden per variabele. Voor p splitsen we het op met de helft van de spaties die zijn ingenomen door T (voor waar) en de andere helft door F (voor onwaar).

Stap 5: Negatie

Voor ~p schrijf je het tegenovergestelde teken dat p heeft aangezien ~p het tegenovergestelde is van p.

Stap 6: Variabele "q"

Voor q wissel je af tussen T en F om elke mogelijke combinatie te krijgen. Omdat de vergelijking alleen gericht is op ~p, kunnen we de p-kolom negeren bij het bepalen van de waarheid van de vergelijking. Het symbool "Λ" betekent dat zowel ~p als q waar moeten zijn om de vergelijking waar te maken.

Stap 7: Oplossen voor False in de laatste kolom

Voor de eerste rij, aangezien ~p F is en q T is, is ~p Λ q F in het scenario dat ~p F is en q T. Het enige scenario dat de vergelijking T is, is waar ~p T is en q T.

Stap 8: Waar vinden in de laatste kolom

Dit betekent dat de enige rij die T is, de derde is.

Stap 9: De tafel afmaken

Controleer nogmaals of uw tabel correct is. Dit doe je door te controleren of je borden goed staan en ervoor te zorgen dat de laatste kolom correct is ingevuld. De laatste kolom is het resultaat van alle mogelijke permutaties van de variabelen.

Stap 10: Klaar

Nu je weet hoe je een eenvoudige waarheidstabel moet maken, moet je blijven oefenen! Hoe meer je oefent, hoe beter je wordt in het doen ervan.