☠WEEDINATOR☠ Deel 4: Differentiële stuurgeometriecode: 3 stappen

2024 Auteur: John Day | [email protected]. Laatst gewijzigd: 2024-01-30 11:18

Als je de tijd hebt om de bovenstaande video te bekijken, zul je merken dat er af en toe vreemde geluiden worden veroorzaakt door de motoren op het stuur die afslaan als de WEEDINATOR een driepuntsbocht navigeert. De motoren lopen in wezen tegen elkaar aan omdat de draaicirkel aan de binnenkant anders is dan aan de buitenkant en de afstand die het wiel aflegt per draaigraad verschilt.

De geometrie van de bocht kan worden uitgewerkt door een achttal permutaties van de bocht te schetsen, waarbij voorbeelden worden gegeven van draaien onder verschillende hoeken op het binnenwiel van 0 (geen bocht) tot 90 (volledige vergrendeling) graden. Klinkt ingewikkeld?

De meeste kleine wielrobots proberen geen enkele vorm van geavanceerde besturing en vertrouwen, zeer effectief, op het eenvoudig veranderen van de relatieve snelheid van de motoren aan elke kant van het voertuig, wat vrijwel hetzelfde is als hoe een rupsgraafmachine of tank werken. Dit is geweldig als je over een met krater gevuld oorlogsgebied aan het schieten bent op alles wat beweegt, maar in een rustige agrarische omgeving is het belangrijk om zo min mogelijk schade aan de grond en de grond aan te richten, zodat slijpschijven heen en weer tegen elkaar zijn. niet geschikt!

De meeste auto's en tractoren hebben een heel handig gadget dat 'Differential' wordt genoemd, behalve de auto's die je in oude Amerikaanse films ziet, waar je de banden als een gek giert elke keer dat ze een bocht om gaan. Bouwen Amerikanen nog steeds zulke auto's? Met de WEEDINATOR kunnen we differentieel in de aandrijfmotoren programmeren door de formule uit te werken voor de relatieve snelheden en hoeken van de wielen bij een bepaalde draaihoek. Klinkt nog steeds ingewikkeld?

Hier is een snel voorbeeld:

Als de WEEDINATOR een bocht navigeert en het binnenste wiel op 45 graden heeft, is het buitenste wiel NIET 45 graden, het is meer 30 graden. Ook kan het binnenste wiel met 1 km/uur draaien, maar het buitenste wiel zal aanzienlijk sneller zijn, ongeveer 1,35 km/uur.

Stap 1: Geometrie instellen

Om te beginnen worden enkele basisaannames gedaan:

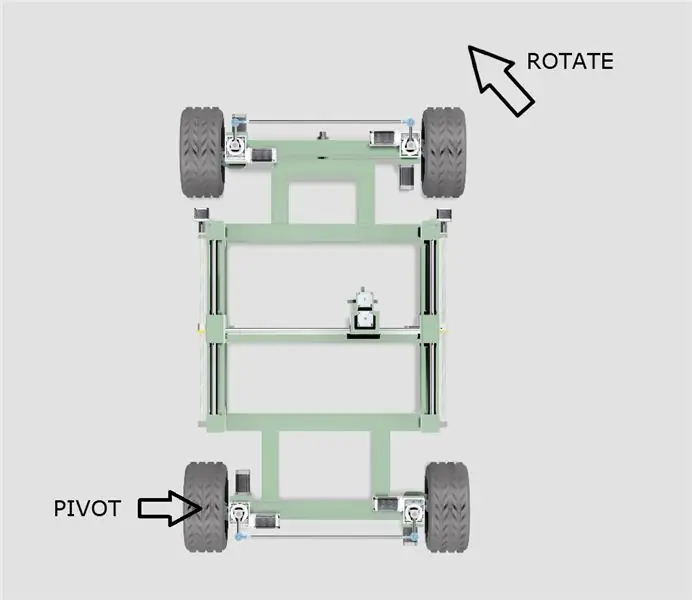
• Het chassis zal rond een van de achterwielen draaien, zoals weergegeven in het bovenstaande diagram.
• Het effectieve middelpunt van de draaicirkel zal bewegen langs een lijn die zich uitstrekt vanaf de middelpunten van de twee achterwielen, afhankelijk van de draaihoek.
• De geometrie zal de vorm aannemen van een sinuscurve.

Stap 2: Geschaalde tekeningen van wielhoeken en radii

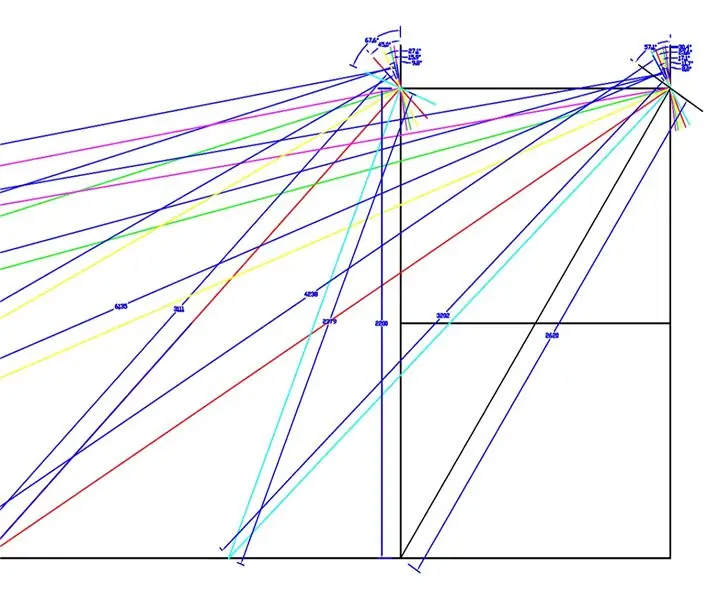
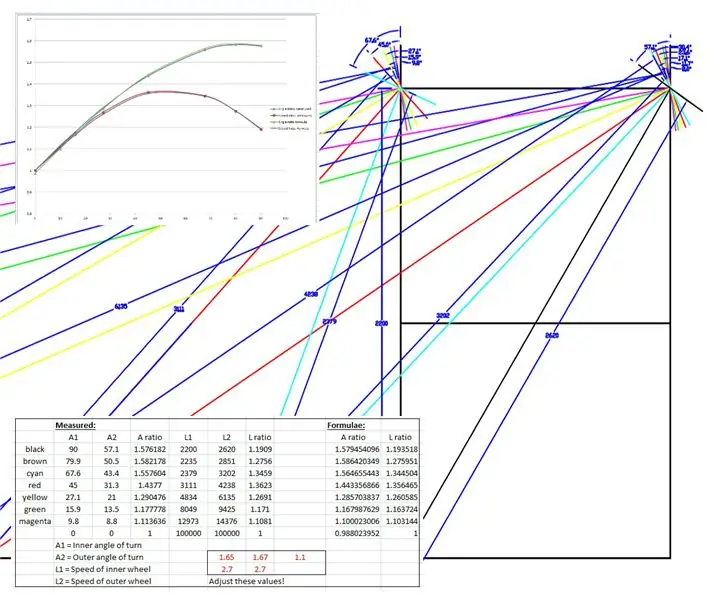
Er is een tekening op ware grootte gemaakt van de WEEDINATOR-voorwielen en het chassis met 8 verschillende permutaties van de binnenste wielhoek tussen 0 en 90 graden en de respectieve draaicentra zijn in kaart gebracht zoals weergegeven in de bovenstaande tekeningen.

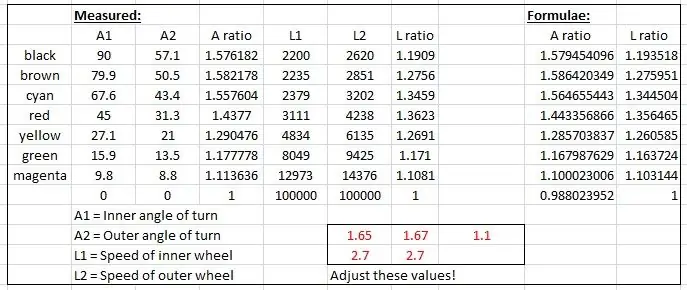
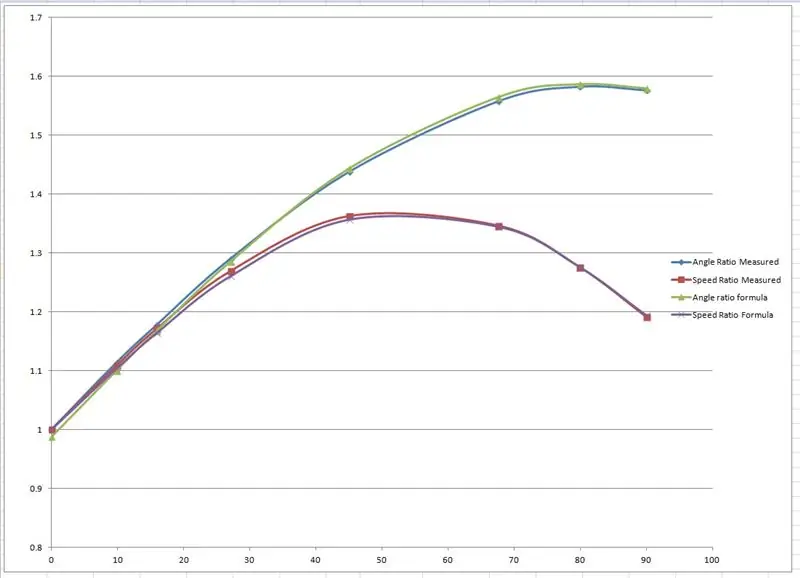
De effectieve stralen werden gemeten vanaf de tekening en uitgezet in een grafiek in Microsoft Excel.

Er werden twee grafieken gemaakt, een van de verhouding van de linker- en rechtervoorwielassen en een andere van de verhouding van de twee stralen voor elke specifieke draaihoek.

Ik heb toen een aantal formules 'verprutst' om de empirische resultaten na te bootsen op basis van een sinuscurve. Een van de fudges ziet er als volgt uit:

speedRatio= (sin(inner*1.65*pi/180)+2.7)/2,7; // inner is de binnenste draaihoek.

De curven werden geknoeid door de rood weergegeven waarden in het Excel-bestand te wijzigen totdat de curven in elkaar pasten.

Stap 3: De formules coderen

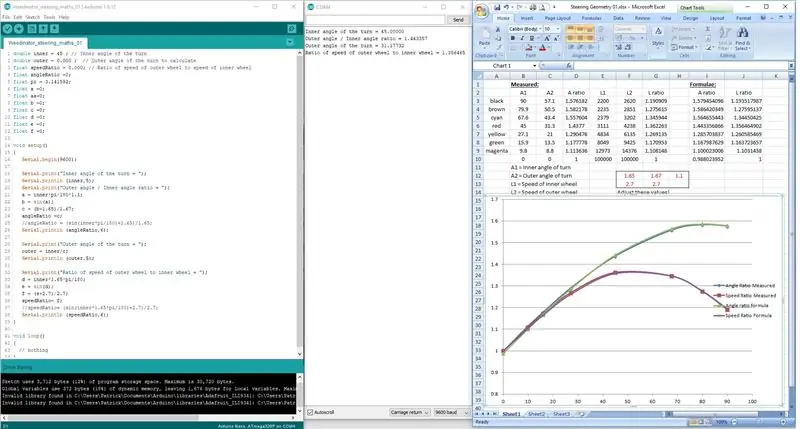
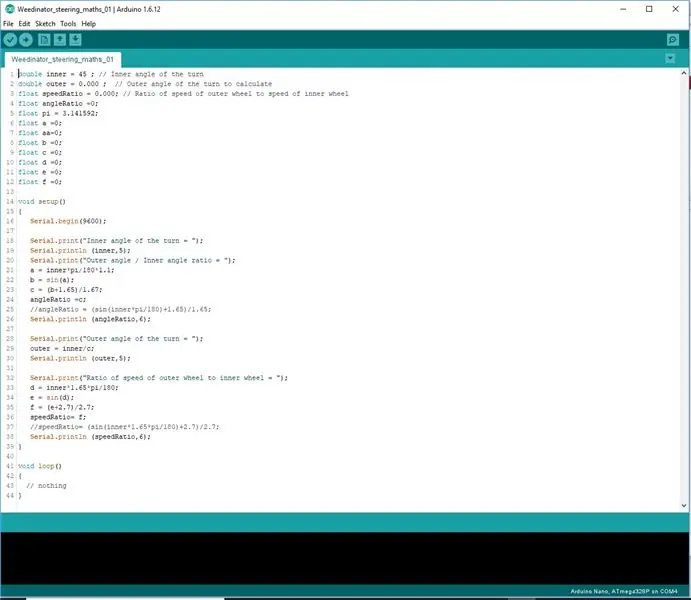
In plaats van te proberen de formules in één regel te coderen, werden ze opgesplitst in 3 fasen zodat de Arduino de wiskunde goed kon verwerken.

De resultaten worden weergegeven op het display van de seriële poort en gecontroleerd met de meetresultaten op de schaaltekening.