CNC-drumplotter - Ajarnpa

2024 Auteur: John Day | [email protected]. Laatst gewijzigd: 2024-01-30 11:16

Deze instructable beschrijft een A4/A3-plotter gemaakt van een stuk plastic pijp, twee BYJ-48 stappenmotoren en een SG-90 servo. In wezen is het een flat-bed plotter opgerold in een trommel.

De ene motor laat de trommel draaien terwijl de andere de printkop beweegt. De servo wordt gebruikt om de pen omhoog en omlaag te brengen.

Deze plotter heeft een aantal voordelen ten opzichte van een traditionele flatbed plotter:

• aanzienlijk kleinere voetafdruk
• vereist slechts één lineaire geleiderail
• eenvoudig te construeren
• goedkoop

Een ingebouwde tolk accepteert de gcode-uitvoer van Inkscape.

Communicatie met de plotter gaat via een bluetooth link.

De plotter is compatibel met de CNC Graphics Tablet beschreven in mijn instructable

Hoewel het geen precisie-instrument is, is de nauwkeurigheid van deze plotter bevredigend voor het beoogde doel van het overbrengen van aquarelcontouren op papier.

Stap 1: Het circuit

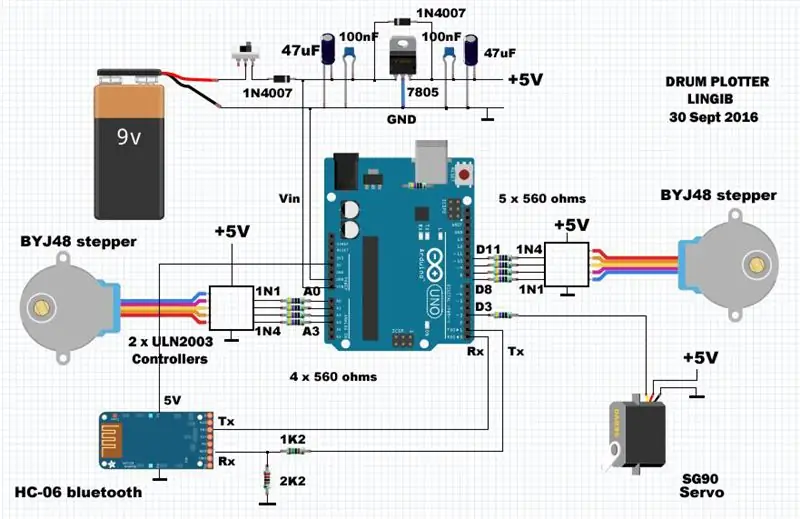
Het circuit bestaat uit een Arduino UNO R3-microcontroller en een custom shield waarop de discrete componenten zijn gemonteerd. De stroom wordt geleverd via een externe 5 volt 1 amp-regelaar. De gemiddelde stroom is ongeveer 500mA.

De BYJ-48 stappenmotoren zijn bevestigd aan PORTB (pinnen D8, D9, D10, D11) en PORTC (pinnen A0, A1, A2, A3). De SG-90 pen-lift servo is bevestigd aan pin D3.

De weerstanden van 560 ohm, die kunnen worden weggelaten, bieden een mate van kortsluitbeveiliging aan de arduino als er iets misgaat. Ze maken het ook gemakkelijker om de afscherming te bedraden, omdat ze als "jumpers" over de voedingsrails werken.

De 1k2- en 2K2-weerstanden voorkomen schade aan de HC-06 bluetooth-module [1] door de 5 volt-uitgang van de arduino te verlagen tot 3,3 volt.

[1] Koppel de HC-06 bluetooth-module los bij het uploaden van code naar de Arduino via de USB-poort. Dit voorkomt eventuele seriële poortconflicten.

Stap 2: De lineaire aandrijving

De lineaire aandrijving is gemaakt van een lengte van 3 mm x 32 mm aluminium staaf, een strook aluminiumplaat en vier kleine kogelgelagerde katrollen.

Het aluminium is verkrijgbaar bij de meeste bouwmarkten. De U624ZZ 4x13x7mm U-groef katrollen zijn verkrijgbaar bij

Eenvoudig handgereedschap is alles wat u nodig heeft. Snijd de aluminium balk op maat van uw plotterafmetingen.

De motorassemblage

Monteer de BJY-48 stappenmotor door de staaf aan het ene uiteinde en bevestig een GT2 20 tand, 5 mm boring, poelie aan de motoras. Monteer nu nog een GT2-poelie aan het andere uiteinde van je stang zodat de poelie vrij kan draaien. Ik heb hiervoor een buisvormige (radio) spacer met een diameter van 5 mm en een bout van 3 mm gebruikt.

Lus nu een stuk GT2-distributieriem om de poelies. Verbind de tandriemuiteinden door middel van een halve draai zodat de tanden in elkaar schuiven en fixeren met een kabelbinder.

Bevestig tenslotte de wagenconstructie met een kabelbinder aan de distributieriem.

Het rijtuig assemblage

Het wagensamenstel is gemaakt van een strook aluminiumplaat [1] waarop de U624ZZ-poelies zijn vastgeschroefd. Gebruik indien nodig een ring van 4 mm om de katrollen op afstand van de aluminium plaat te plaatsen.

De katrollen, die een groef van 4 mm hebben, schrijlings op de aluminium staaf boven en onder zodat er geen verticale beweging is, maar de aluminium strip beweegt vrij naar links en rechts.

Om ervoor te zorgen dat de slede vrij kan lopen, monteer je eerst de bovenste twee katrollen en markeer je vervolgens, met de katrollen op de stang, de posities van de onderste twee katrollen. De gaten voor deze twee katrollen kunnen nu worden geboord. Gebruik eerst een kleine "pilot"-boor om te voorkomen dat de grotere boor van 4 mm afdrijft.

Voordat u de aluminiumstrip in een "U" buigt, boort u een gat aan de boven- en onderkant om de diameter van uw pen aan te passen. Maak nu de bochten af.

Bevestig de distributieriem aan de wagenconstructie door middel van een kabelbinder en een bout van 3 mm tussen de bovenste twee poelies.

De pen-lift montage

Bevestig een SG-90-servo aan de bovenkant van de wagenconstructie met behulp van een of twee kabelbinders.

Laat je pen in de twee gaten vallen die je hebt geboord. Zorg ervoor dat de pen vrij op en neer kan glijden.

Bevestig een "kraag" aan uw pen zodat de pen net uit de trommel komt wanneer de servo in de pen-up positie staat.

[1] Aluminium kan worden gesneden door beide zijden van de plaat in te snijden met een scherp mes (doosmes) en de snede vervolgens over de rand van een tafel te buigen. Een paar keer wiebelen en het laken zal breken en een rechte breuk achterlaten. In tegenstelling tot tin-snips knikt deze methode het aluminium niet.

Stap 3: De trommel

De trommel bestaat uit een stuk kunststof buis met twee houten eindpluggen [1].

Gebruik een kompas, ingesteld op de binnenradius van uw pijp, om de contouren van de eindpluggen te tekenen. Snijd nu rond elke omtrek met een fijne zaag ("coping", "fret") en monteer vervolgens elke eindplug op maat met behulp van een houtrasp. Bevestig de eindpluggen met kleine verzonken houtschroeven.

Een technische bout van 6 mm door het midden van elke eindplug vormt de as.

Afmetingen trommel

De afmetingen van de drum worden bepaald door uw papierformaat. Een trommeldiameter van 100 mm ondersteunt A4 staand en A3 liggend. Een trommeldiameter van 80 mm ondersteunt alleen A4 liggend. Gebruik een zo klein mogelijke trommeldiameter om de traagheid te verminderen … de BYJ-48-motoren zijn maar klein.

Een trommeldiameter van 90 mm is ideaal voor A4-portret- en A3-landschapspapier, aangezien de tegenovergestelde randen, wanneer ze om de trommel worden gewikkeld, ongeveer 10 mm overlappen, wat betekent dat u maar één naad hoeft te plakken.

De trommel draaien

Elke as loopt door een aluminium eindbeugel zodat de trommel vrij kan draaien. Eindvlotter wordt voorkomen door middel van een GT-2, 20 tanden, 6 mm boring, poelie die aan één uiteinde aan de as is bevestigd. Een doorlopende GT-2-distributieriem verbindt de BJY-48-stappenmotor met de trommel. De motor vereist een katrol met een boring van 5 mm.

[1] Kunststof eindpluggen zijn beschikbaar voor de meeste buisdiameters, maar werden afgewezen omdat ze over de buis passen in plaats van erin en het plastic de neiging heeft om te buigen. Ze zouden waarschijnlijk in orde zijn als er een doorlopende as zou worden gebruikt in plaats van de bouten … maar dan heb je een methode nodig om de as aan de eindpluggen te bevestigen.

Stap 4: Bouwtips

Zorg ervoor dat de pen langs het midden van de trommel beweegt. Dit kan worden bereikt door de hoeken uit de houten steunen te snijden. Als de pen niet in het midden staat, zal deze de neiging hebben om langs de zijkant van de trommel naar beneden te glijden.

Nauwkeurig boren van de twee pengaten is belangrijk. Wiebelen in de pengeleider of sledeconstructie zullen wiebelen langs de X-as veroorzaken.

Span de GT-2-distributieriemen niet te strak aan … ze moeten gewoon strak staan. BYJ-48 stappenmotoren hebben niet veel koppel.

BJY-48 stappenmotoren vertonen vaak kleine hoeveelheden speling die onbeduidend is langs de X-as, maar een punt van zorg is als het gaat om de Y-as. De reden hiervoor is dat één omwenteling van de Y-asmotor gelijk staat aan één omwenteling van de trommel, terwijl de penwagen vele omwentelingen van de X-asmotor nodig heeft om de lengte van de trommel te doorlopen. Elke speling op de Y-as kan worden geëlimineerd door een constant koppel op de trommel te houden. Een eenvoudige methode is om een klein gewicht te bevestigen aan een nylon koord dat om de trommel is gewikkeld.

Stap 5: Bresenham's lijntekeningalgoritme

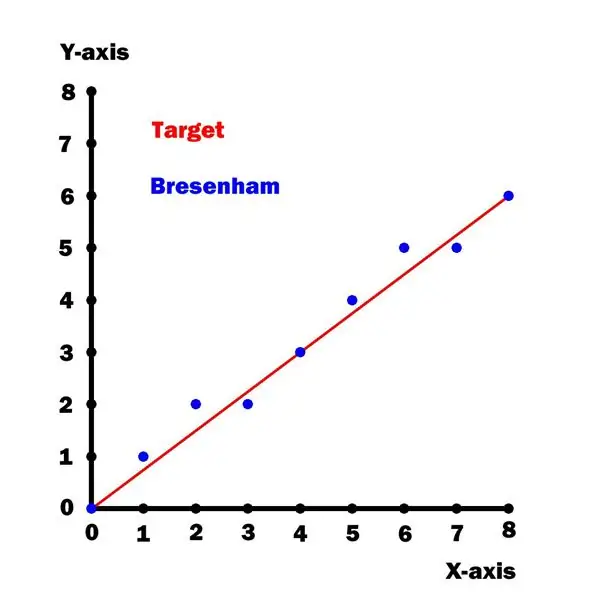
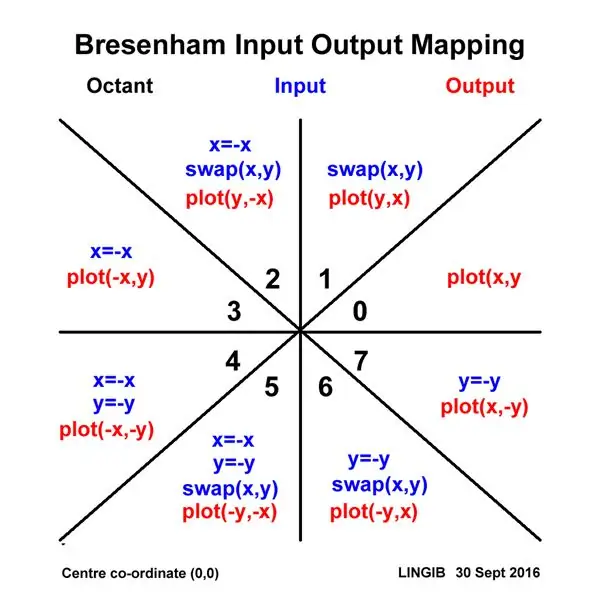
Deze plotter gebruikt een geoptimaliseerde versie [1] van het lijntekeningalgoritme van Bresenham. Helaas is dit algoritme alleen geldig voor lijnhellingen kleiner dan of gelijk aan 45 graden (d.w.z. één octant van een cirkel).

Om deze beperking te omzeilen, "map" ik alle XY-ingangen naar het eerste "octant" en "unmap" ze vervolgens wanneer het tijd is om te plotten. De invoer- en uitvoertoewijzingsfuncties om dit te bereiken, worden weergegeven in het bovenstaande diagram.

Afleiding

De rest van deze stap kan worden overgeslagen als u bekend bent met het algoritme van Bresenham.

Laten we een lijn trekken van (0, 0) naar (x1, y1) waarbij:

• x1=8=horizontale afstand
• y1=6=verticale afstand

De vergelijking voor een rechte lijn door de oorsprong (0, 0) wordt gegeven door de vergelijking y=m*x waarbij:

m=y1/x1=6/8=0,75=helling

Eenvoudig algoritme

Een eenvoudig algoritme om deze lijn te plotten is:

• int x1=8;
• int y1=6;
• vlotter m=y1/x1;
• perceel(0, 0);
• voor (int x=1; x<=x1; x++) {
• int y=rond (m*x);
• plot (x, y);
• }

Tabel 1: Eenvoudig algoritme

x	m	m*x	ja
0	0.75	0	0
1	0.75	0.75	1
2	0.75	1.5	2
3	0.75	2.25	2
4	0.75	3	3
5	0.75	3.75	4
6	0.75	4.5	5
7	0.75	5.25	5
8	0.75	6	6

Er zijn twee problemen met dit eenvoudige algoritme:

• de hoofdlus bevat een vermenigvuldiging die traag is
• het gebruikt drijvende-kommagetallen die ook traag zijn

Een grafiek van y versus x voor deze lijn is hierboven weergegeven.

Het algoritme van Bresenham

Bresenham introduceerde het concept van een foutterm 'e' die wordt geïnitialiseerd op nul. Hij realiseerde zich dat de in tabel 1 getoonde m*x-waarden verkregen kunnen worden door achtereenvolgens 'm' aan 'e' toe te voegen. Hij realiseerde zich verder dat y alleen wordt opgehoogd als het fractionele deel van m*x groter is dan 0,5. Om zijn vergelijking binnen het bereik 0<=0.5<=1 te houden, trekt hij 1 af van 'e' wanneer y wordt verhoogd.

• int x1=8;
• int y1=6;
• vlotter m=y1/x1;
• int y=0;
• vlotter e=0;
• perceel(0, 0);
• voor (int x=1; x<=x1; x++) {
• e+= m;
• als (e>= 0,5) {
• e-= 1;
• y++;
• }
• plot (x, y);
• }

Tabel 2: Algoritme van Bresenham

x	m	e	e-1	ja
0	0.75	0	0	0
1	0.75	0.75	-0.25	1
2	0.75	0.5	-0.5	2
3	0.75	0.25		2
4	0.75	1	0	3
5	0.75	0.75	-0.25	4
6	0.75	0.5	-0.5	5
7	0.75	0.25		5
8	0.75	1	0	6

Als je het algoritme en tabel 2 bekijkt, zie je dat;

• de hoofdlus gebruikt alleen optellen en aftrekken … er is geen vermenigvuldiging
• het patroon voor y is hetzelfde als voor tabel 1.

Maar we gebruiken nog steeds drijvende-kommagetallen … laten we dit oplossen.

Het (geoptimaliseerde) algoritme van Bresenham

Het drijvende-kommaalgoritme van Bresenham kan worden omgezet in een geheel getal als we 'm' en 'e' met 2*x1 schalen, in welk geval m=(y1/x1)*2*x1=2*y1

Afgezien van het schalen van 'm' en 'e' is het algoritme vergelijkbaar met dat hierboven, behalve:

• we voegen 2*y1 toe aan 'e' elke keer dat we 'x' verhogen
• we verhogen y als e gelijk is aan of groter is dan x1.
• we trekken 2*x1 af van 'e' in plaats van 1
• x1 wordt gebruikt voor de vergelijking in plaats van 0,5

De snelheid van het algoritme kan verder worden verhoogd als de lus nul gebruikt voor de test. Om dit te doen, moeten we een offset toevoegen aan de foutterm 'e'.

• int x1=8;
• int y1=6;
• int m=(y1<<1); //constant: helling geschaald met 2*x1
• int E=(x1<<1); //constant: 2*x1 voor gebruik in lus
• int e = -x1; //offset van -E/2: test nu gedaan op nul
• perceel(0, 0);
• int y=0;
• voor (x=1; x<=x1; x++) {
• e += m;
• als (e>=x1) {
• e -= E
• y++;
• }
• plot (x, y);
• }

Tabel 3: Bresenham's (geoptimaliseerde) algoritme

x	m	E	e	e - E	ja
0	12	16	-8		0
1	12	16	4	-12	1
2	12	16	0	-16	2
3	12	16	-4		2
4	12	16	8	-8	3
5	12	16	4	-12	4
6	12	16	0	-16	5
7	12	16	-4		5
8	12	16	8	-8	6

Nogmaals, het patroon voor y is hetzelfde als in de andere tabellen. Het is interessant op te merken dat tabel 3 alleen gehele getallen bevat en dat de verhouding van m/E=12/16=0,75 de helling 'm' van de lijn is.

Dit algoritme is extreem snel omdat de hoofdlus alleen bestaat uit optellen, aftrekken en een vergelijking met nul. Vermenigvuldiging wordt niet gebruikt, behalve wanneer we de waarden voor 'E' en 'm' initialiseren met behulp van een "links-shift" om de waarden van x1 en y1 te verdubbelen.

[1] Deze geoptimaliseerde versie van het algoritme van Bresenham is afkomstig uit een paper "Bresenham Line and Circle Drawing", copyright © 1994-2006, W Randolph Franklin (WRF). Zijn materiaal mag worden gebruikt voor onderzoek en onderwijs zonder winstoogmerk, op voorwaarde dat u hem crediteert en een link naar zijn startpagina,

Stap 6: De code

Download het bijgevoegde bestand naar een map met dezelfde naam en upload het vervolgens naar de plotter met behulp van uw arduino IDE (geïntegreerde ontwikkelomgeving).

Koppel de HC-06 bluetoorh-module los voordat u probeert te uploaden. Dit is nodig om een seriële poortconflict met de USB-kabel te voorkomen.

Code van derden

Naast de bovenstaande.ino-code heeft u de volgende softwarepakketten nodig die gratis / donatie-ware zijn:

• Teraterm die beschikbaar is op
• Inkscape die beschikbaar is op

Instructies voor het installeren en gebruiken van elk van de bovenstaande pakketten van derden zijn te vinden in mijn artikel

Stap 7: Menu

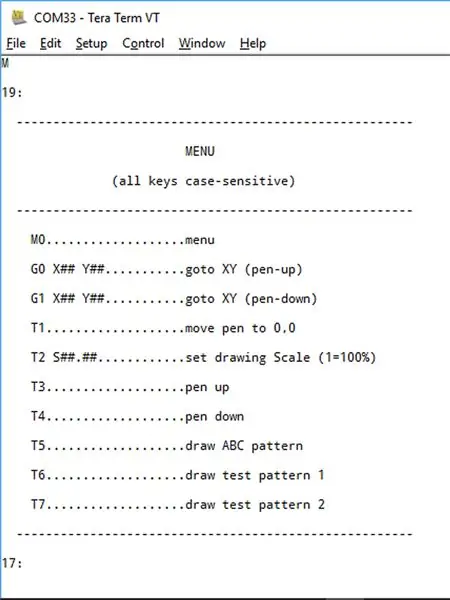
Maak een bluetooth-verbinding met uw plotter met behulp van "Teraterm".

Zet je "caps lock" aan want alle commando's zijn in hoofdletters.

Typ de letter 'M' en een menu zou moeten verschijnen zoals hierboven weergegeven.

Het menu spreekt redelijk voor zich:

• M (of M0) roept het menu op
• Met G0 kunt u de pen naar een specifieke XY-coördinaat sturen met de pen omhoog.
• Met G1 kunt u de pen naar een specifieke XY-coördinaat sturen met de pen omlaag.
• Met T1 kunt u uw pen over uw 0, 0-coördinaat plaatsen. Typ 'E' om af te sluiten.
• Met T2 kunt u uw tekening schalen. "T2 S2.5" zal uw tekening bijvoorbeeld 250% schalen. De standaardschaal is 100%
• Met T3 en T4 kunt u de pen omhoog of omlaag brengen.
• T5 tekent een "ABC"-testpatroon.
• T6 tekent een "doel".
• T7 tekent een reeks radiale lijnen, waarvan het doel is om te controleren of het algoritme van Bresenham werkt in elk van de acht "octanten"

Opmerkingen:

• alle penbewegingen gebruiken de tekenschaalset met menuoptie T2
• de "17:" en "19:" nummers zijn de "Xon" en "Xoff" terminal handshake codes van de Arduino interpreter.

Stap 8: Kalibratie

De waarden voor X_STEPS_PER_MM en Y_STEPS_PER_MM zijn voor een trommel met een diameter van 90 mm.

Waarden voor andere trommeldiameters kunnen worden berekend met behulp van de volgende relaties:

• de omtrek van de trommel is PI*diameter;
• 2048 stappen is gelijk aan één omwenteling van elke motoras
• één omwenteling van een GT-2-poelie staat gelijk aan 40 millimeter lineaire beweging van een distributieriem

Een andere methode is om de volgende opdrachten in te voeren,

• G1 X0 Y100
• G1 X100 Y100

meet vervolgens de lengte van de resulterende lijnen en "schaal" de waarden voor X-STEPS_PER_MM en Y_STEPS_PER_MM

Stap 9: Gcode-voorverwerking

Deze plotter vereist slechts vier van de Inkscape gcodes (nl.: G0, G1, G2, G3). De code wordt aanzienlijk sneller uitgevoerd als we alle onnodige gcodes en opmerkingen verwijderen.

Om dit te doen heeft u een kopie van "Notepad++" nodig. Deze gratis teksteditor bevat een "reguliere expressie"-zoekmachine voor het vinden en verwijderen van ongewenste tekst. Notepad++ is beschikbaar via

Open het te wijzigen bestand met Notepad++ en plaats uw cursor bovenaan het bestand.

Selecteer "Bekijken/Toon symbool/Alle tekens" gevolgd door "Zoeken/vervangen…" in de bovenste menubalk.

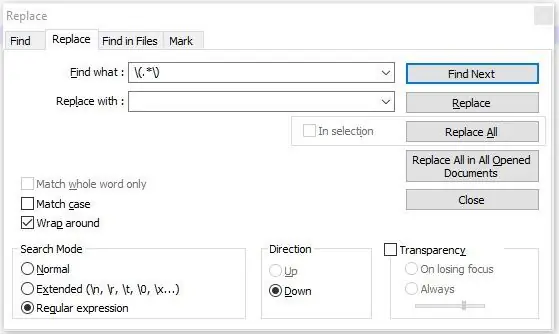
Klik op het selectievakje "Reguliere expressie" (zie 1e afbeelding) en voer elk van de volgende codereeksen in het zoekvak in.

Klik op "Alles vervangen" na elk item:

• %
• (.*)
• ^M.*$
• Z.*$

De bovenstaande reguliere expressies verwijderen alle %-symbolen, alle opmerkingen tussen haakjes, alle M-codes, alle Z-codes en de codes die volgen.

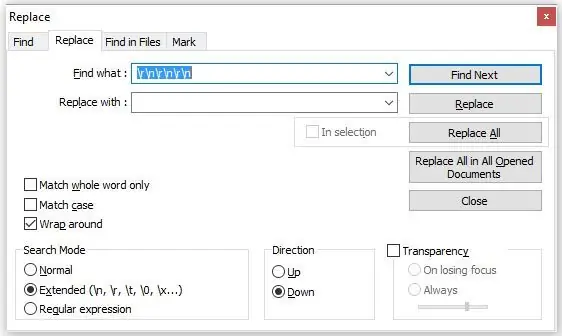
Klik nu op het selectievakje "Extended Expression" (zie 2e afbeelding) en voer de volgende codereeks in:

r\n\r\n\r\n

Deze uitdrukking verwijdert de ongewenste regelterugloop en regelinvoer die door de eerste reeks zijn gemaakt.

Sla je bestand op onder een andere naam met "Opslaan als".

Gedaan.

Stap 10: Resultaten

Deze plotter is gebouwd als "proof of concept" en nooit bedoeld om perfect te zijn. Dat gezegd hebbende, de resultaten zijn niet al te slecht. Ze voldoen zeker aan mijn ontwerpdoel om aquarelcontouren op papier over te brengen.

De eerste drie afbeeldingen zijn respectievelijk de ingebouwde testpatronen T5, T6, T7.

De "Hallo wereld!" patroon werd via bluetooth naar de plotter gestuurd. Een "voorverwerkte" kopie van dit bestand is bijgevoegd.

Stap 11: Code-update

De code voor deze plotter is bijgewerkt naar Drum_Plotter_V2.ino.

Wijzigingen ten opzichte van de originele Drum_Plotter.ino zijn onder meer:

• soepelere penpositionering
• herkent nu G02 gcode-instructies (bogen met de klok mee)
• herkent nu G03 gcode-instructies (bogen tegen de klok in)

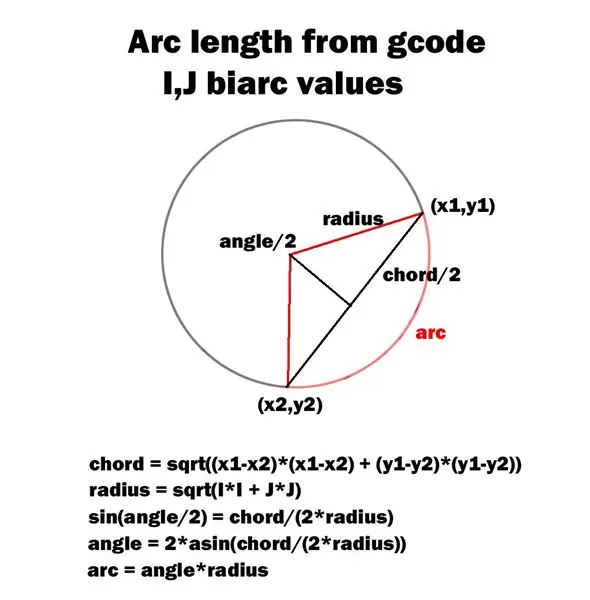
Het bijgevoegde diagram schetst mijn methode voor het berekenen van de booghoek.

Stap 12: Drum_plotter_v3.ino

Een code-update voor "CNC Drum Plotter" is bijgevoegd.

"drum_plotter_v3.ino" repareert een kleine bug die de nauwkeurigheid van de plotter beïnvloedde.

Verander geschiedenis

Versie 2:

Bi-boogkrommen toegevoegd

Versie 3:

De volgende functies zijn herschreven om een kleine fout aan te pakken die de nauwkeurigheid van de plotter beïnvloedde.

• (int) vervangen door round() in de move_to() functie.
• draw_line() functie "octant" zoekalgoritme verbeterd
• De interpreter gebruikt nu stringfuncties in plaats van pointers, wat het ontwerp vereenvoudigt. We kunnen nu bijvoorbeeld zoeken naar "MENU" in plaats van te zoeken naar de letter 'M' en vervolgens het gehele getal eruit halen dat volgt. Hierdoor kunt u de plotter personaliseren met uw eigen commando's.

Stap 13: Drum_plotter_plotter_v4.ino

16 januari 2017:

De code voor deze drumplotter is verder geoptimaliseerd. Er zijn extra functies toegevoegd.

De wijzigingen omvatten:

• sneller draw_line() algoritme
• overeenkomende move_to() functie
• stappentellers
• kleine bug opgelost

Lees voor meer informatie de opmerkingen in "drum_plotter_v4.ino" bijgevoegd.

Klik hier om mijn andere instructables te bekijken.