Zelfbalancerende robot met PID-algoritme (STM MC) - Ajarnpa

2024 Auteur: John Day | [email protected]. Laatst gewijzigd: 2024-01-30 11:18

De laatste tijd is er veel werk verzet aan het zelfbalanceren van objecten. Het concept van zelfbalancering begon met het balanceren van de omgekeerde slinger. Dit concept breidde zich ook uit tot het ontwerpen van vliegtuigen. In dit project hebben we een klein model van een zelfbalancerende robot ontworpen met behulp van het PID-algoritme (Proportional, Integral, Derivative). Sindsdien is deze methode het nieuwe gezicht van de industriële procesbesturingssystemen. Dit rapport geeft een overzicht van de methoden die betrokken zijn bij het zelfbalanceren van objecten. Dit project werd uitgevoerd als een semesterproject om de correlatie van PID op de efficiëntie van verschillende industriële processen te begrijpen. Hier richten we ons alleen op het geven van een kort overzicht van de eectiviteit en toepassing van de PID-regeling. Dit document is ontwikkeld door een korte inleiding te geven over besturingssystemen en gerelateerde terminologieën, met toevoeging van de motivaties voor het project. Er zijn experimenten en observaties gedaan, voor- en nadelen beschreven met als eindpunt de toekomstige verbeteringen. Er is een model van een zelfbalancerende robot ontwikkeld om de effectiviteit van PID in de wereld van regelsystemen te begrijpen. Na enkele rigoureuze tests en experimenten werden de voor- en nadelen van het PID-regelsysteem ontdekt. Het bleek dat ondanks de vele voordelen van PID-regeling ten opzichte van eerdere methoden, dit systeem nog steeds veel verbeteringen vereist. Gehoopt wordt dat de lezer een goed begrip krijgt van het belang van zelfbalancering, de eectiviteit en tekortkomingen van PID-regeling

Stap 1: Inleiding

Met de komst van computers en de industrialisatie van processen is er in de hele geschiedenis van de mens altijd onderzoek geweest om manieren te ontwikkelen om processen te verfijnen en, belangrijker nog, om ze autonoom te besturen met behulp van machines. Het doel is om de betrokkenheid van de mens bij deze processen te verminderen, waardoor de fouten in deze processen worden verminderd. Daarom is het vakgebied "Control System Engineering" ontwikkeld. Control System Engineering kan worden gedefinieerd als het gebruik van verschillende methoden om de werking van een proces of het onderhoud van een constante en geprefereerde omgeving te controleren, of dit nu handmatig of automatisch is.

Een eenvoudig voorbeeld is het regelen van de temperatuur in een ruimte. Handmatige besturing betekent de aanwezigheid van een persoon op een locatie die de huidige omstandigheden controleert (sensor), deze vergelijkt met de gewenste waarde (verwerking) en passende actie onderneemt om de gewenste waarde te verkrijgen (actuator). Het probleem met deze methode is dat deze niet erg betrouwbaar is, aangezien een persoon vatbaar is voor fouten of nalatigheid in zijn werk. Een ander probleem is ook dat de snelheid van het proces dat door de actuator wordt gestart niet altijd uniform is, wat betekent dat het soms sneller kan gebeuren dan vereist of dat het soms langzaam kan zijn. De oplossing van dit probleem was om een microcontroller te gebruiken om het systeem te besturen. De microcontroller is

geprogrammeerd om het proces te regelen, volgens bepaalde specificaties, aangesloten in een circuit (later te bespreken), gevoed met de gewenste waarde of condities en bestuurt daardoor het proces om de gewenste waarde te behouden. Het voordeel van dit proces is dat er geen menselijke tussenkomst nodig is in dit proces. Ook is de snelheid van het proces uniform

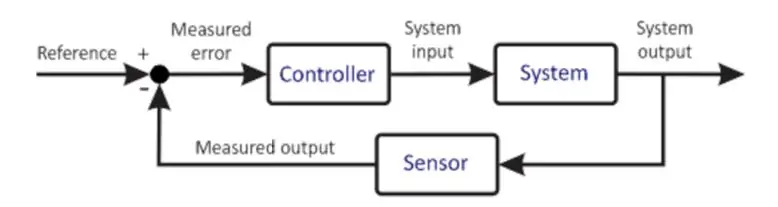
Basisbesturingssysteem

Het vorige diagram toont een zeer vereenvoudigde versie van een besturingssysteem. De microcontroller vormt het hart van elk besturingssysteem. Het is een zeer belangrijk onderdeel, daarom moet de keuze van de selectie zorgvuldig worden gemaakt op basis van de vereisten van het systeem. De microcontroller krijgt input van de gebruiker. Deze ingang bepaalt de gewenste toestand van het systeem. De microcontroller ontvangt ook een feedback-invoer van de sensor. Deze sensor wordt aangesloten op de uitgang van het systeem, waarvan de informatie wordt teruggekoppeld naar de ingang. De microprocessor voert op basis van zijn programmering verschillende berekeningen uit en geeft een output aan de actuator. De actuator stuurt op basis van de output de installatie aan om te proberen die omstandigheden te handhaven. Een voorbeeld kan een motoraandrijver zijn die een motor aandrijft waarbij de motoraandrijver de actuator is en de motor de installatie. De motor draait dus met een bepaalde snelheid. De aangesloten sensor leest de huidige toestand van de installatie en stuurt deze terug naar de microcontroller. De microcontroller vergelijkt opnieuw, maakt berekeningen en zo herhaalt de cyclus zich. Dit proces is repetitief en eindeloos waarbij de microcontroller de gewenste omstandigheden handhaaft

Stap 2: PID-gebaseerd regelsysteem

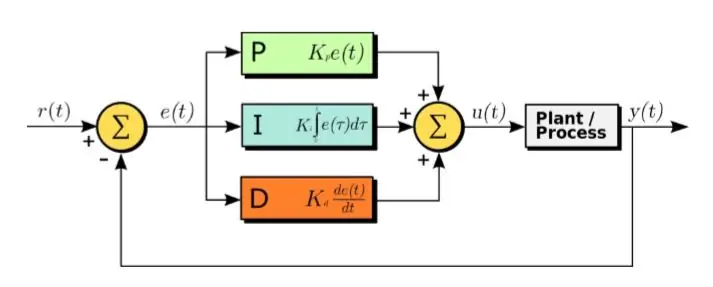
Het PID-algoritme is een eciënte methode om een regelsysteem te ontwerpen.

definitie

PID staat voor Proportioneel, Integraal en Derivatief. In dit algoritme is het ontvangen foutsignaal de invoer. En de volgende vergelijking wordt toegepast op het foutsignaal:

U(t) = Kp∗e(t) + Kd∗d/dt(e(t)) + Ki∗integraal(e(t)) (1,1)

Korte uitleg

Zoals te zien is in de bovenstaande vergelijking, worden de integraal en afgeleide van de foutsignalen berekend, vermenigvuldigd met hun respectieve constanten en opgeteld samen met de constante Kp vermenigvuldigd met e(t). De output wordt vervolgens naar de actuator gevoerd die het systeem laat draaien. Laten we nu eens naar elk onderdeel van de functie kijken. Deze functie is direct van invloed op de stijgtijd, daaltijd, peak-overshoot, insteltijd en steady-state-fout.

• Proportioneel deel: Het proportionele deel vermindert de stijgtijd en vermindert de stationaire fout. Dit betekent dat het systeem minder tijd nodig heeft om zijn piekwaarde te bereiken en wanneer het zijn stabiele toestand bereikt, zal de stationaire fout laag zijn. Het verhoogt echter de piekoverschrijding.

• Afgeleide deel: Het afgeleide deel vermindert de overshoot en de afwikkelingstijd. Dit betekent dat de transiënte toestand van het systeem meer gedempt zal zijn. Ook zal het systeem in minder tijd zijn stabiele toestand bereiken. Het heeft echter geen effect op de stijgtijd of de stationaire fout.

• Integraal onderdeel: het integrale onderdeel verkort de stijgtijd en elimineert de stationaire fout volledig. Het verhoogt echter de piekoverschrijding en de insteltijd.

• Afstemming: een goed regelsysteem heeft een lage stijgtijd, insteltijd, piekoverschrijding en steady-state-fout. Daarom moeten de Kp, Kd, Ki nauwkeurig worden afgesteld om de bijdrage van de bovengenoemde factoren aan te passen om een goed regelsysteem te verkrijgen.

Er is een afbeelding bijgevoegd die het effect toont van het wijzigen van verschillende parameters in het PID-algoritme.

Stap 3: Zelfbalancerende robot

Een zelfbalancerende robot is een meerlagige robot op twee wielen.

De robot zal proberen zichzelf in evenwicht te brengen bij toepassing van ongelijke kracht(en). Het zal zichzelf in evenwicht brengen door kracht uit te oefenen die de resultante van de krachten op de robot tegenwerkt.

Methoden voor zelfbalancering

Er zijn vier methoden voor zelfbalancering van robots. Deze zijn als volgt:

Zelfbalancerend met behulp van twee IR-kantelsensoren

Dit is een van de meest primitieve manieren om de robot in evenwicht te brengen, omdat er minder hardware en een relatief eenvoudig algoritme voor nodig is. Bij deze benadering worden twee gekantelde IR-sensoren gebruikt om de afstand tussen de grond en de robot te meten. Op basis van de berekende afstand kan PID worden gebruikt om de motoren aan te drijven om de robot dienovereenkomstig te balanceren. Een nadeel van deze methode is dat de IR-sensor enkele metingen kan missen. Een ander probleem is dat een interrupt en lussen nodig zijn voor de berekening van de afstand, wat de tijdcomplexiteit van het algoritme vergroot. Daarom is deze manier van balanceren van de robot niet erg eciënt.

Zelfbalancerend met behulp van Accelerometer

Accelerometer geeft ons de versnelling van het lichaam in 3 assen. Versnelling gericht op de y-as (naar boven) en x-as (vooruit) geeft ons de maat om de richting van de zwaartekracht te berekenen en dus de hellingshoek te berekenen. De hoek wordt als volgt berekend:

θ = arctan(Ay/Ax) (1,2)

Het nadeel van het gebruik van deze methode is dat tijdens de beweging van de robot de horizontale versnelling ook wordt opgeteld bij de meetwaarden, wat een hoogfrequent geluid is. De hellingshoek zal dus onnauwkeurig zijn.

Zelfbalanceren met gyroscoop

Een gyroscoop wordt gebruikt om de hoeksnelheden langs de drie assen te berekenen. De hellingshoek wordt verkregen met behulp van de volgende vergelijking.

θp(i) = θp(i−1) + 1/6(vali−3 + 2vali−2 + 2vali−1 + vali) (1.3)

Een groot nadeel van het gebruik van de gyroscoop is dat deze een kleine DC-bias heeft, wat een laagfrequente ruis is en binnen een paar keer zijn de geretourneerde waarden volledig verkeerd. Hierdoor zal na integratie het nulpunt wegdrijven. Hierdoor zal de robot enige tijd in verticale positie blijven en zal omvallen zodra de drift komt.

Zelfbalancerend met zowel versnellingsmeter als gyroscoop

Zoals hierboven besproken, zal het gebruik van alleen een versnellingsmeter of gyroscoop ons niet de juiste hellingshoek geven. Om dat te verklaren, worden zowel de versnellingsmeter als de gyroscoop gebruikt. Deze zijn beide ingebed in MPU6050. Hierin verkrijgen we de gegevens van beide en fuseren ze vervolgens door Kalman-filter of complementair filter te gebruiken.

• Kalman-filter: het Kalman-filter berekent de beste schatting van de toestand van een dynamisch systeem op basis van metingen met ruis, waardoor de gemiddelde kwadratische fout van de schatting wordt geminimaliseerd. Het werkt in twee fasen, voorspelling en correctie, gezien de discrete stochastische vergelijkingen die de systeemdynamiek beschrijven. Het is echter een zeer complex algoritme om te implementeren, vooral op een beperkte hardware van een microcontroller.

• Complementair filter: dit algoritme gebruikt voornamelijk de gegevens die zijn verkregen van de gyroscoop en integreert deze in de loop van de tijd om de hellingshoek te bepalen. Het gebruikt ook een klein deel van de versnellingsmeterwaarden. Het complementaire filter minimaliseert in feite het hoogfrequente geluid van de accelerometer en het laagfrequente geluid van de gyroscoop en voegt ze vervolgens samen om de best nauwkeurige hellingshoek te verkrijgen.

Stap 4: Ontwerp van robot

We hebben een zelfbalancerende robot ontworpen met behulp van een proportionele afgeleide controller, geïmplementeerd door Complementary Filter voor MPU6050. Dit kleine model van Self Balancing Robot zal ons het nut illustreren van controlesystemen in Self Balancing van robots.

Systeemimplementatie:

Het systeem is een zelfbalancerende robot. Het wordt geïmplementeerd met behulp van de PID-controller, een proportionele integrale afgeleide controller. We balanceren de robot door zijn wielen in de richting van zijn val te laten rijden. Daarbij proberen we het zwaartepunt van de robot boven het draaipunt te houden. Om de wielen in de richting van zijn val te laten rijden, moeten we weten waar de robot valt en met welke snelheid hij valt. Deze gegevens worden verkregen met behulp van MPU6050 die een versnellingsmeter en een gyroscoop heeft. MPU6050 meet de hellingshoek en geeft zijn output aan de Micro-Controller. MPU6050 is via I2C verbonden met het STM-bord. In I2C is één draad voor de klok die wordt genoemd als SCL. De andere is voor de gegevensoverdracht die SDA is. Hierbij wordt gebruik gemaakt van master slave communicatie. Startadres en eindadres zijn gespecificeerd om te weten waar de gegevens beginnen en waar ze eindigen. We hebben hier het complementaire filter geïmplementeerd voor MPU6050, een wiskundig filter om de uitgangen van versnellingsmeter en gyroscoop samen te voegen. Na het verkrijgen van de gegevens van de MPU6050, voert de microcontroller berekeningen uit om te weten waar hij valt. Op basis van de berekeningen zal de STM-microcontroller de motorbestuurder opdrachten geven om de voertuigen in de valrichting te rijden, waardoor de robot in evenwicht wordt gebracht.

Stap 5: Projectcomponenten

De volgende componenten zijn gebruikt in het zelfbalancerende robotproject:

STM32F407

Een microcontroller ontworpen door ST Microelectronics. Het werkt op de ARM Cortex-M-architectuur.

Motorstuurprogramma L298N

Dit IC wordt gebruikt om de motor te laten draaien. Het krijgt twee externe ingangen. Een van de microcontroller die hem een PWM-signaal levert. Door de breedte van de puls aan te passen, kan de motorsnelheid worden aangepast. De tweede ingang is de spanningsbron die nodig is om de motor aan te drijven, in ons geval een 12V-batterij.

DC-motor

Een DC-motor draait op een DC-voeding. In dit experiment draait de DC-motor met behulp van de optocouplers die op de motordriver zijn aangesloten. Om de motor aan te drijven hebben we de Motor Drive L298N gebruikt.

MPU6050

MPU6050 wordt gebruikt om informatie te krijgen over waar de robot valt. Het meet de hellingshoek ten opzichte van het nulpunt dat de positie is van de MPU6050 wanneer het programma begint te lopen.

De MPU6050 heeft een 3-assige versnellingsmeter en een 3-assige gyroscoop. De versnellingsmeter meet de versnelling langs de drie assen en de gyroscoop meet de hoeksnelheid rond de drie assen. Om de output te combineren, moeten we de geluiden van beide filteren. Om de geluiden te filteren, hebben we Kalman en Complementair filter. We hebben Complementair filter in ons project geïmplementeerd.

Opto Koppel 4N35

Een optocoupler is een apparaat dat wordt gebruikt om het laagspanningsgedeelte en het hoogspanningsgedeelte van het circuit te isoleren. Zoals de naam al doet vermoeden, werkt het op basis van licht. Wanneer het laagspanningsgedeelte een signaal krijgt, vloeit er stroom in het hoogspanningsgedeelte

Stap 6: Structuur van robot

De structuur van de robot wordt als volgt uitgelegd:

Fysieke structuur

De zelfbalancerende robot bestaat uit twee lagen van transparant kunststof glas. De details van twee lagen worden hieronder gegeven:

Eerste laag

In het onderste deel van de eerste laag hebben we een cel geplaatst om het STM-bord van stroom te voorzien. Ook zijn er aan elke kant twee motoren van elk 4 volt geplaatst met banden die zijn aangesloten om de robot te laten bewegen. In het bovenste deel van de eerste laag zijn twee accu's van elk 4 volt (8 volt totaal) en motordriver IC (L298N) geplaatst voor de werking van motoren.

Tweede laag

In de bovenste laag van de robot hebben we het STM Board op Perf Board geplaatst. Op de toplaag wordt nog een perfboard van 4 opto couplers geplaatst. Gyroscoop wordt ook vanaf de onderkant op de bovenste laag van de robot geplaatst. Beide componenten zijn in het middendeel geplaatst zodat het zwaartepunt zo laag mogelijk wordt gehouden.

Zwaartepunt van robot

Het zwaartepunt wordt zo laag mogelijk gehouden. Hiervoor hebben we zware batterijen op de onderste laag geplaatst en lichte componenten zoals STM-board en optocouplers op de bovenste laag.

Stap 7: Coderen

Code is gecompileerd op Atollic TrueStudio. STM studio werd gebruikt voor foutopsporingsdoeleinden.

Stap 8: Conclusie

Na veel experimenteren en observeren komen we uiteindelijk op het punt dat we onze resultaten samenvatten en bespreken in hoeverre we erin geslaagd zijn de effectiviteit van het systeem te implementeren en uit te werken.

Algemene beoordeling

Tijdens de experimenten werd de snelheid van de motor met succes geregeld met behulp van het PID-algoritme. De curve is echter niet bepaald een vloeiende rechte lijn. Daar zijn veel redenen voor:

• De sensor, hoewel aangesloten op een laagdoorlaatfilter, geeft nog steeds bepaalde eindige debounces; deze zijn te wijten aan de niet-lineaire weerstanden en enkele onvermijdelijke redenen van de analoge elektronica.

• De motor draait niet soepel onder kleine spanning of PWM. Het levert schokken op die ertoe kunnen leiden dat verkeerde waarden aan het systeem worden toegevoerd.

• Door wiebelen kan de sensor enkele sleuven missen die hogere waarden opleveren. • Een andere belangrijke reden voor fouten kan de kernklokfrequentie van de STM-microcontroller zijn. Dit model van STM-microcontroller biedt een kernklok van 168 MHz. Hoewel dit probleem in dit project is behandeld, bestaat er een algemeen idee over dit model dat het niet echt zo'n hoge frequentie biedt.

De open loop-snelheid zorgt voor een zeer vloeiende lijn met slechts een paar onverwachte waarden. Het PID-algoritme werkt ook prima en biedt een zeer korte insteltijd van de motor. Het PID-algoritme van de motor werd getest onder verschillende spanningen, waarbij het referentietoerental constant werd gehouden. De spanningsverandering verandert de snelheid van de motor niet, wat aantoont dat het PID-algoritme goed werkt

Eectiviteit

Hier bespreken we de eectiviteit van de PID-controller die we tijdens de experimenten hebben waargenomen.

Eenvoudige implementatie

We hebben in de sectie experimenten en observaties gezien dat een PID-controller heel eenvoudig te implementeren is. Er zijn slechts drie parameters of constanten nodig die moeten worden ingesteld om een snelheidsregelsysteem te hebben

Ongeëvenaarde efficiëntie voor lineaire systemen

Lineaire PID-regelaar is de meest eciënte in de familie van regelaars omdat de logica heel eenvoudig is en de toepassing wijdverbreid is in het geval van lineaire of vrij lineaire toepassingen.

Beperkingen

We hebben in het abstract uitgelegd wat de beperkingen van dit systeem zijn. Hier bespreken we er een paar die we hebben waargenomen.

Selectie van constanten

We hebben gezien dat, hoewel een PID-regelaar eenvoudig te implementeren is, het toch een groot nadeel van het systeem is dat de stap van het selecteren van de waarde van constanten een moeizame stap is; als men moeilijke berekeningen moet maken. De andere manier is de hit and trial-methode, maar ook dat is niet eciënt.

Constanten niet altijd constant

De experimentele resultaten toonden aan dat voor verschillende waarden van de referentiesnelheid voor de motor, de PID-regelaar niet goed functioneerde voor dezelfde waarden van de PID-constanten. Voor verschillende snelheden moesten de constanten anders worden gekozen en dit verhoogt de rekenkosten exponentieel.

Niet-lineair

De PID-regelaar die in ons geval wordt gebruikt, is lineair en kan daarom alleen op lineaire systemen worden toegepast. Voor niet-lineaire systemen moet de controller anders worden geïmplementeerd. Hoewel er verschillende niet-lineaire PID-methoden beschikbaar zijn, moeten er meer parameters worden geselecteerd. Dit maakt het systeem opnieuw ongewenst vanwege de hoge rekenkosten.

Initiële push vereist

We hebben in het experimentgedeelte aangetoond dat voor een vrij kleine referentiesnelheid waarbij de fout in het begin vrij klein is, de door de PID geleverde PWM zo klein is dat deze niet het vereiste startkoppel voor de motor genereert. Zo loopt de motor in sommige proeven niet of in andere proeven zorgt voor een grote overshoot en een langere insteltijd.

Stap 9: Speciale dank

Speciale dank aan mijn groepsleden die me door dit project hebben geholpen.

Ik zal de link naar de video binnenkort uploaden.

Ik hoop dat je dit instructable interessant vindt.

Dit is Tahir Ul Haq van UET die zich afmeldt. Proost !!!