Temperatuur meten vanaf PT100 met Arduino: 6 stappen (met afbeeldingen)

2024 Auteur: John Day | [email protected]. Laatst gewijzigd: 2024-01-31 10:23

De PT100 is een weerstandstemperatuurdetector (RTD) die zijn weerstand verandert afhankelijk van de omgevingstemperatuur, hij wordt veel gebruikt voor industriële processen met een langzame dynamiek en relatief brede temperatuurbereiken. Het wordt gebruikt voor langzame dynamische processen omdat RTD's langzame responstijden hebben (waar ik later meer over vertel), maar nauwkeurig zijn en weinig drift vertonen in de loop van de tijd. Wat ik je in deze Instructable ga laten zien, zou niet voldoen aan de industriële standaard, maar het zal je blootstellen aan een alternatieve manier om de temperatuur te meten dan het gebruik van de LM35 waar veel hobbyisten bekend mee zouden zijn en de getoonde circuittheorie kan worden toegepast op andere sensoren.

Stap 1: Componenten

1x PT100 (twee draden)

1x Arduino (elk model)

3x 741 bedrijfsversterkers (LM741 of UA741)

1x 80ohm Weerstand

2x 3.9kohm weerstanden

2x 3.3kohm weerstanden

2x 8,2kohm weerstanden

2x 47kohm weerstanden

1x 5kohm Potentiometer

1x voeding met twee aansluitingen of 8x 1,5 V AA-batterijen

Ik gebruik een tweedraads PT100, drie- en vierdraads PT100's hebben verschillende circuits. De weerstandswaarden voor de meeste hiervan hoeven niet exact hetzelfde te zijn als hierboven, maar als er een paar weerstanden is, dat wil zeggen de 3,9 Kohms, als je ze verwisselt voor laten we zeggen 5k, moet je beide omwisselen voor 5k als dan hetzelfde moeten zijn. Als we de schakeling krijgen, zal ik zeggen wat het effect is van het kiezen van verschillende waarden. Voor de operationele versterkers (opamps) kun je andere opamps gebruiken, maar dit zijn degene die ik heb gebruikt.

Stap 2: Wheatstone-brug

Ik moet het eerst hebben over de formule om de temperatuur uit de weerstand voor de PT100 te halen voordat ik het heb over het eerste deel van het circuit, de formule voor de weerstand is als volgt:

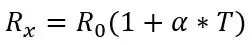
waarbij Rx de PT100-weerstand is, R0 de PT100-weerstand bij 0 graden C, α de temperatuurweerstandscoëfficiënt en T de temperatuur.

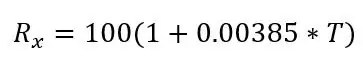
R0 is 100 ohm aangezien dit een PT100 is, als het een PT1000 was, zou R0 1000 ohm zijn. α is 0,00385 ohm/graden C uit de datasheet. Er is ook een nauwkeurigere formule die hier te vinden is, maar de bovenstaande formule is geschikt voor dit project. Als we de formule transponeren, kunnen we de temperatuur voor een gegeven weerstand berekenen:

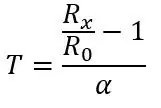
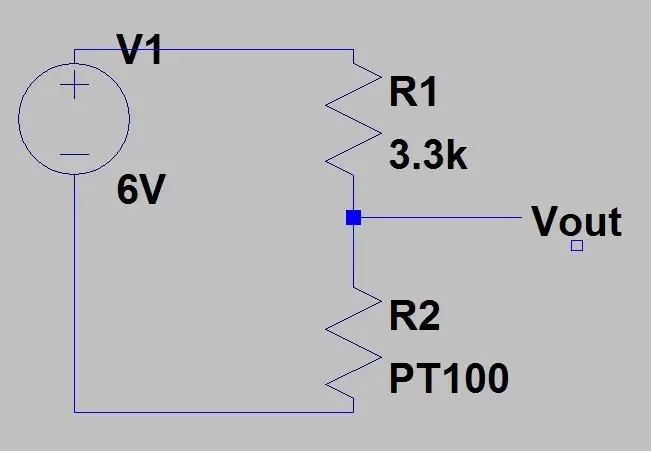
Laten we zeggen dat we iets willen meten met een temperatuurbereik van -51,85 tot 130 graden C en we plaatsten de PT100 in het circuit getoond in afbeelding 1. Met behulp van de bovenstaande vergelijking en de vergelijking voor de spanning uit een spanningsdeler (getoond in de eerste afbeelding) kunnen we het spanningsbereik berekenen. Onderkant van het bereik T = -51,85 (80 ohm)

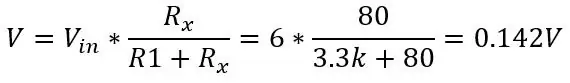
en bij 130 graden (150ohm):

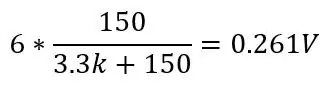
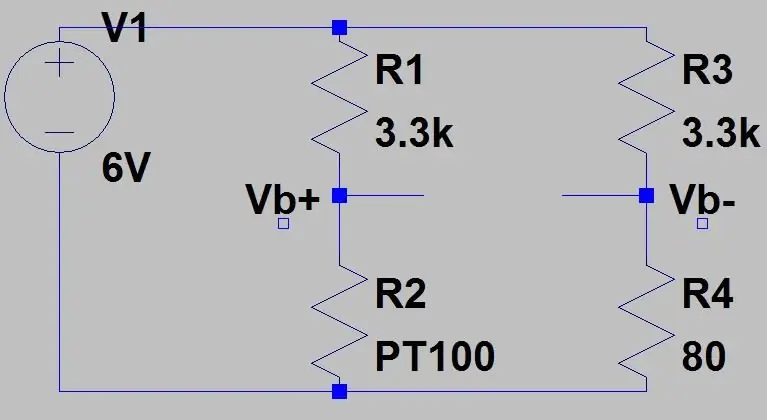
Dit zou een bereik geven van 0,1187V en een DC-offset van 0,142 omdat we weten dat onze temperatuur nooit onder -51,85 graden C zal komen, dit zal de gevoeligheid verminderen in het bereik waar we om geven (80 tot 130 ohm) wanneer we deze spanning versterken. Om van deze DC-offset af te komen en onze gevoeligheid te vergroten, kunnen we een Wheatstone-brug gebruiken die op de tweede afbeelding wordt getoond.

De uitvoer van de tweede spanningsdeler (Vb-) wordt later met een differentiële versterker afgetrokken van de eerste spanningsdeleruitgang (Vb+). De formule voor de uitgang van de brug is slechts twee spanningsdelers:

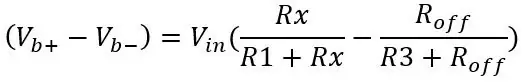
De uitgangsspanning voor de PT100 is 80 ohm en gebruikt de andere waarden in de afbeelding:

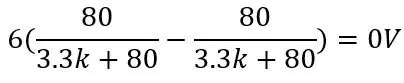
en voor Pt100 van 150 ohm:

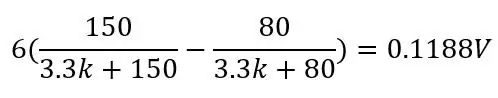
Door gebruik te maken van de Wheatstone halen we de DC-offset weg en verhogen we de gevoeligheid na versterking. Nu we weten hoe de Wheatstone-brug werkt, kunnen we praten over waarom we 80 ohm en 3,3 kohm gebruiken. De 80ohm wordt een beetje uitgelegd aan de hand van de bovenstaande formule, kies deze waarde (we noemen dit de offset-weerstand Roff) om het onderste bereik van je temperatuur te zijn of zelfs beter, iets onder het onderste van je bereik, als dit wordt gebruikt voor een regelsysteem voor temperatuurregeling of iets dergelijks, je zou willen weten hoe laag de temperatuur onder je temperatuurbereik komt. Dus als -51.85C de onderkant van uw bereik is, gebruik dan 74.975 ohm (-65 graden C) voor uw Roff.

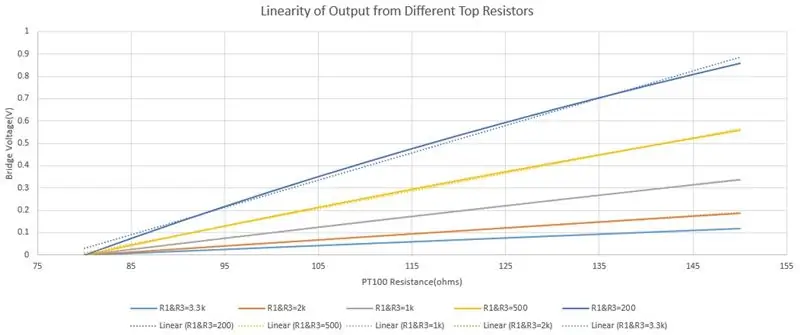
Ik koos 3.3k voor R1 en R3 om twee redenen, om de stroom te beperken en de lineariteit van de output te vergroten. Omdat de weerstand van de PT100 verandert als gevolg van de temperatuur, zal het doorlaten van te veel stroom onjuiste metingen geven vanwege zelfverhitting, dus koos ik een maximale stroomsterkte van 5-10 mA. Wanneer de PT100 80 ohm is, is de stroom 1.775 mA, dus veilig onder het maximale bereik. Je verlaagt de weerstand om de gevoeligheid te vergroten, maar dit kan een negatief effect hebben op de lineariteit, omdat we later de vergelijking van een lijn zullen gebruiken (y=mx+c) met een niet-lineaire uitvoer zal fouten introduceren. De derde afbeelding heeft een grafiek van de bruguitgang met verschillende topweerstanden, de ononderbroken lijn is de werkelijke uitvoer en de stippellijn is de lineaire benadering. U kunt zien dat in de donkerblauwe grafiek (R1&R3=200ohms) het grootste spanningsbereik wordt weergegeven, maar de uitvoer is het minst lineair. De lichtblauwe (R1 & R3 = 3,3 kohms) geeft het kleinste spanningsbereik, maar de stippellijn en de ononderbroken lijn overlappen elkaar, wat aangeeft dat de lineariteit erg goed is.

Voel je vrij om deze waarden aan te passen aan je toepassing, ook als je de spanning verandert, zorg er dan voor dat de stroom niet te hoog wordt.

Stap 3: Versterking

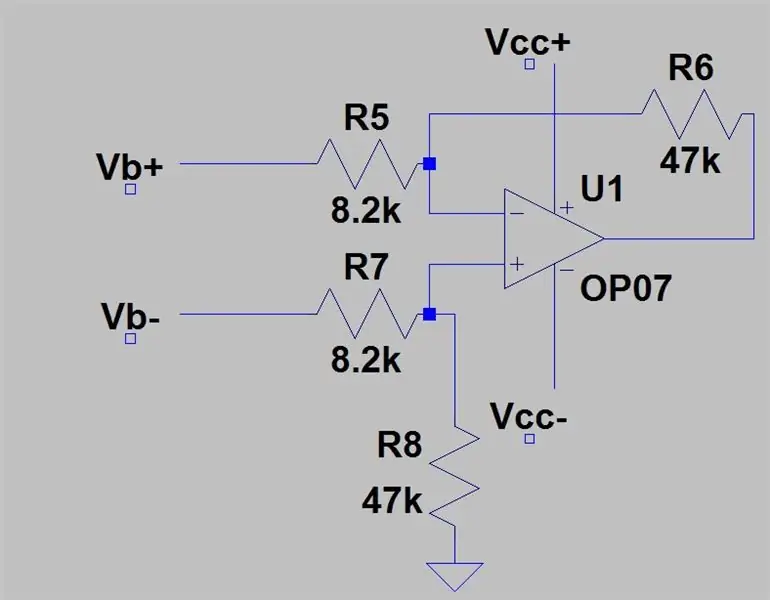
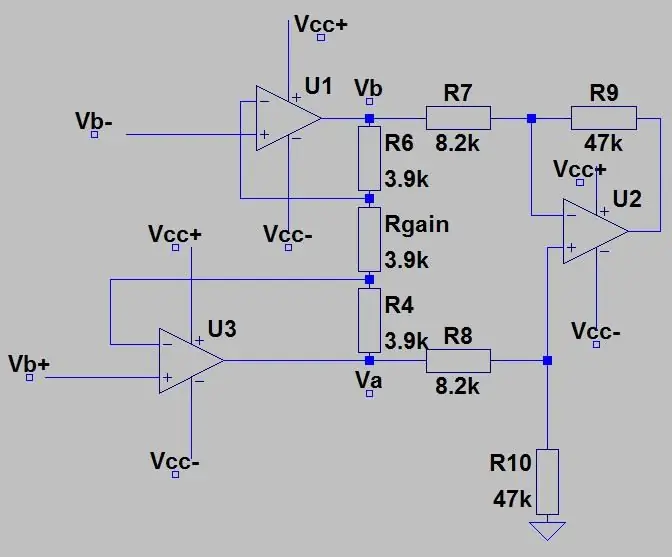
In de laatste stap ontdekten we dat het uitgangsbereik van de twee afgetrokken spanningsdelers 0 tot 0,1187 was, maar we hebben niet gesproken over het aftrekken van deze spanningen. Om dit te doen hebben we een differentiële versterker nodig die de ene ingang van de andere aftrekt en deze versterkt met de versterking van de versterker. Het circuit voor een differentiële versterker wordt getoond in de eerste afbeelding. Je voert de Vb + in de inverterende ingang en Vb- in de niet-inverterende ingang en de uitgang zal de Vb + - Vb- zijn met een versterking van één, dus geen versterking, maar door de weerstanden toe te voegen die in de afbeelding worden getoond, voegen we een versterking toe van 5.731. De winst wordt gegeven door:

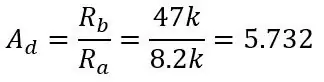
Ra is R5 & R7 en Rb is R6 & R8, de spanning wordt gegeven door:

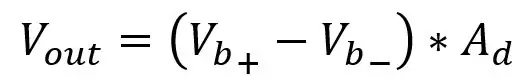
Er zijn twee problemen met het aansluiten van deze versterker op de uitgang van de brug, het laadeffect en het veranderen van de versterking. Het veranderen van de versterking van de versterker vereist dat je ten minste twee weerstanden verandert, aangezien de twee paar weerstanden hetzelfde moeten zijn, dus het zou vervelend zijn om twee potten te hebben die dezelfde waarde moeten hebben, dus gebruiken we iets dat een instrumentatieversterker wordt genoemd waarover ik het hieronder heb. Het laadeffect is dat de ingangsweerstanden in de versterker de spanningsval over de PT100 beïnvloeden, we willen dat de spanning over de PT100 ongewijzigd blijft en om dit te doen kunnen we zeer grote weerstanden kiezen voor de ingangsweerstanden zodat de parallelle weerstand van de PT100 en ingangsweerstand is zeer dicht bij de PT100-weerstand, maar dit kan problemen veroorzaken met ruis en uitgangsspanningsoffset waar ik niet op in ga. Kies gewoon het middenbereik in het Kohms-bereik, maar zoals ik al zei, het hebben van kleine weerstanden is ook slecht, dus we zullen het circuit een beetje veranderen.

In de tweede afbeelding hebben we de uitgang van de brug aangesloten op een instrumentatieversterker die als bufferversterker fungeert om de twee helften van de circuits (de brug en versterking) te scheiden en waarmee ook de ingang kan worden versterkt door slechts één potentiometer te veranderen (winst). De versterking van de instrumentatieversterker wordt gegeven door:

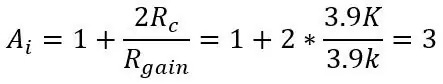
waarbij Rc de twee weerstanden van 3,9 k boven en onder de pot is.

Door Rgain te verlagen, neemt de versterking toe. Dan op punt Va en Vb (versterkte Vb + en Vb-), is het gewoon een differentiële versterker zoals voorheen en de totale versterking van het circuit is gewoon de winst vermenigvuldigd met elkaar.

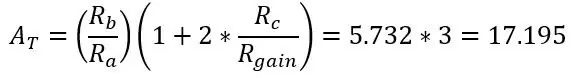
Om je winst te kiezen, wil je iets doen zoals we eerder deden met de Roff, we moeten een weerstand kiezen net boven je maximale temperatuur in je bereik voor het geval deze overschrijdt. Omdat we de Arduino gebruiken die een 5V-adc heeft, moet de maximale output van het circuit 5V zijn bij de maximale temperatuur die je hebt gekozen. Laten we de 150 ohm kiezen omdat de maximale weerstand en de niet-versterkte brugspanning 0,1187V was, de versterking die we nodig hebben is 42,185 (5/0,1187)

Laten we zeggen dat we Ra, Rb en Rc houden als 8,2k, 47k en 3,9k, we moeten alleen de waarde voor de pot Rgain vinden:

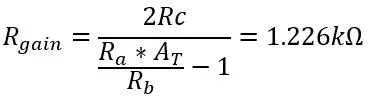
Dus om de volledige 5 volt uit het temperatuurbereik te halen dat we gebruiken, wijzigt u de waarde van Rgain in 1.226k. De uitgangsspanning die uit de differentiële versterker komt, wordt gegeven door:

Stap 4: Het circuit van stroom voorzien

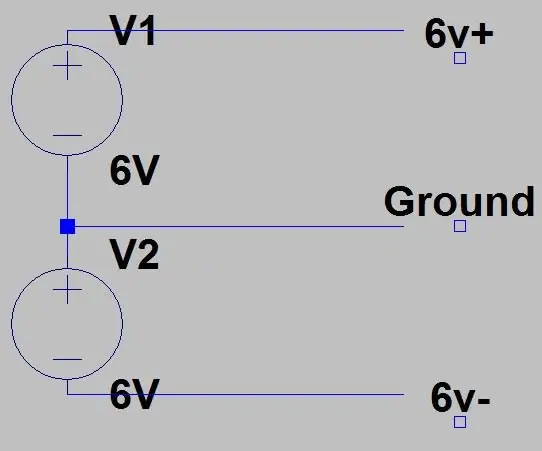
Dit is de laatste stap van het circuit, je hebt misschien de Vcc + en de Vcc- op de opamp-circuits opgemerkt, dit komt omdat ze zowel positieve als negatieve spanning nodig hebben om goed te kunnen functioneren, je kunt single-rail op-amps krijgen, maar ik besloot om deze versterker te gebruiken, want die had ik nog liggen. Dus we leveren +6V en -6V, er zijn drie manieren waarop we dit kunnen doen. De eerste wordt getoond in de eerste afbeelding waar we twee voedingen of twee uitgangsklemmen van een enkele voeding moeten hebben, beide op 6V hebben en een positieve uitgang hebben aangesloten op de negatieve van de andere. De 6V van de bovenste voeding is onze +6V, de positieve van de onderste voeding is de GND en de negatieve van de onderste voeding is de -6V. SLUIT HET ALLEEN ZO ALS DEZE AAN ALS DE GND'S VAN DE TWEE VOEDINGEN GESCHEIDEN ZIJN, OF DIT ZAL JE STROOMVOORZIENING BESCHADIGEN. Alle commerciële voedingen zouden gescheiden GND's hebben, maar als je het wilt controleren, gebruik dan de continuïteitstester op je multimeter, als het zoemt, gebruik dan niet deze opstelling en gebruik de volgende. Op mijn zelfgemaakte voeding, blies ik de zekering door dit te doen.

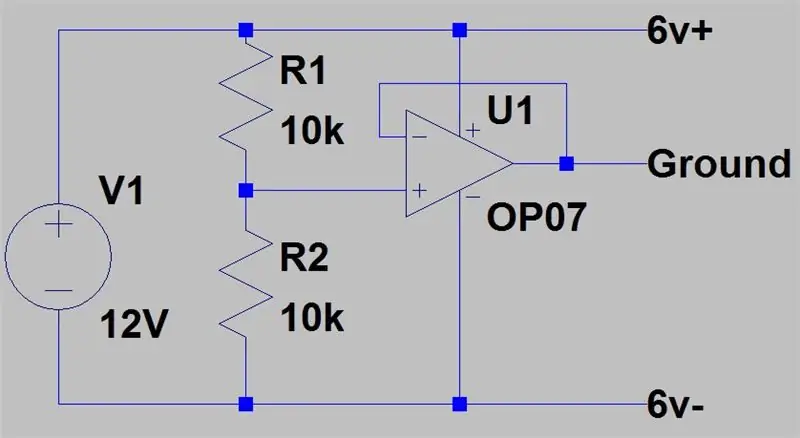
In de tweede afbeelding is de tweede opstelling die we kunnen hebben, het vereist wel dat één voeding het dubbele van de andere spanning heeft, maar zal de voeding niet beschadigen als de GND's zijn aangesloten. We hebben twee voedingen, een op 12V en een andere op 6V. De 12V zal fungeren als onze +6V, de 6V uit de tweede voeding zal fungeren als de GND en de twee werkelijke GND's uit de voeding zullen fungeren als -6V.

Deze laatste opstelling is voor de voedingen met slechts één uitgang, deze gebruikt een bufferversterker van gain 1 om een virtuele aarde te creëren door de helft van de voedingsspanning door de bufferversterker te leiden. Dan zal de 12V fungeren als de +6V en de daadwerkelijke GND-terminal zal -6V zijn.

Als je batterijen wilt gebruiken, raad ik de eerste opstelling aan, maar een probleem met batterijen is dat de spanning zal dalen als ze beginnen te sterven en de spanning uit de brug ook zal dalen, wat verkeerde temperatuurmetingen oplevert. Je kunt natuurlijk de spanning van de accu's aflezen en meenemen in de berekeningen of regelaars en meer accu's gebruiken. Uiteindelijk is het aan jou.

Stap 5: Volledig circuit en code

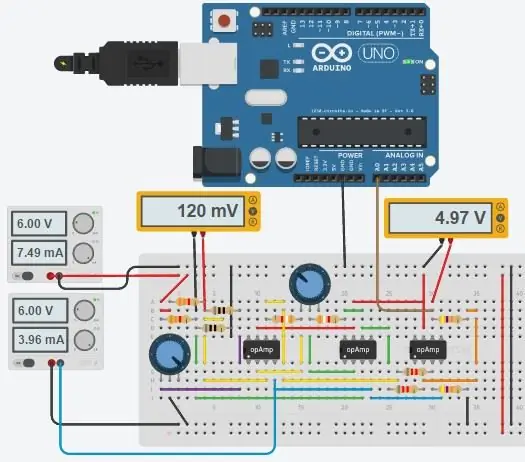
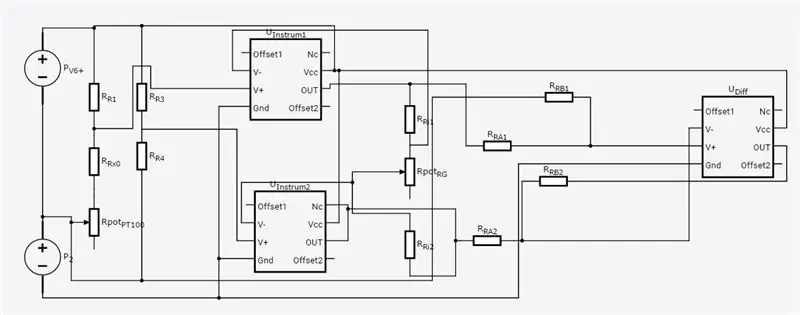
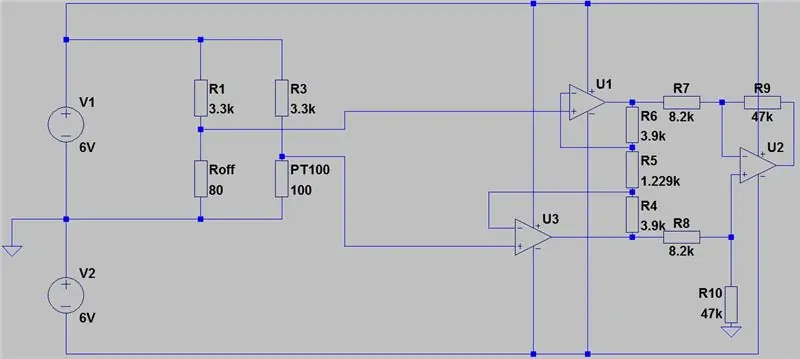
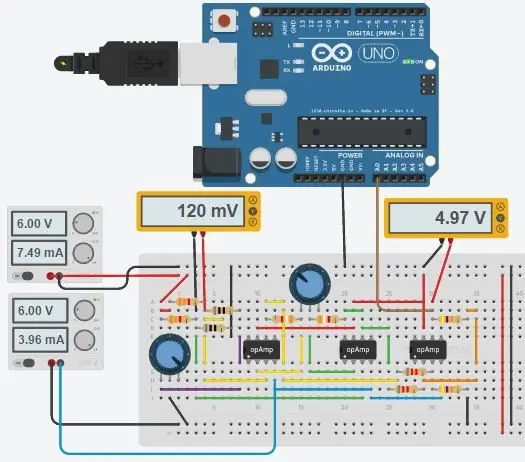
Het volledige circuit is hierboven weergegeven en het is gemaakt in Autodesk's nieuwe Circuits.io, waarmee je circuits op breadboard kunt maken, schakelschema's (getoond in afbeelding 2) en PCB-diagrammen kunt bewerken en het beste deel, laat je het circuit van het breadboard simuleren en kan zelfs een Arduino programmeren en aansluiten in de breadboard-modus, verderop op de pagina staat de simulatie en je kunt met twee potten spelen. Als u het circuit wilt dupliceren en uw eigen waarden wilt invoeren, kunt u het circuit hier vinden. De eerste pot is 70ohm en in serie met een 80ohm weerstand die de PT100 simuleert met een bereik van 80-150ohm, is de tweede pot de gain van de instrumentatieversterker. Helaas heb ik een bibliotheek gebruikt die ik voor mijn code heb gedownload, dus de Arduino is niet opgenomen in het onderstaande circuit, maar er zijn slechts twee extra draden die u hoeft aan te sluiten. Als je meer vertrouwd bent met LTspice, heb ik een asc-bestand bij het circuit gevoegd.

Sluit de A0-pin aan op de uitgang van de differentiële versterker

Verbind de GND van de Arduino met de GND van het circuit (NIET DE -6V)

En dat is het circuit gedaan, nu op de code. Eerder zei ik dat we de formule y=mx+c gaan gebruiken, nu gaan we m(de helling) en c(de offset) berekenen. In de Arduino lezen we de spanning, maar voor de temperatuurvergelijking moeten we de weerstand van de PT100 weten, dus een manier waarop we dit kunnen doen, is door de Serial.println(temp) te vervangen door Serial.println(V) en de spanning en weerstand bij twee temperaturen. Wanneer u deze test doet, laat u de PT100 een tijdje alleen, bijvoorbeeld een minuut of twee, en houdt u hem uit de buurt van warmtebronnen (zonlicht, laptopventilator, uw lichaam, enz.).

Het eerste punt dat we kunnen nemen is kamertemperatuur, wanneer je het circuit hebt aangesloten en werkt, noteer dan de spanning (Vt1) die door de Arduino is gelezen op de seriële monitor en ontkoppel snel de PT100 en noteer de weerstand (Rt1), zet je handen op de sonde bij het loskoppelen, omdat dit de weerstand zal veranderen. Voor de tweede temperatuur kunnen we de sonde in ijswater of heet water plaatsen (wees voorzichtig bij het gebruik van heet water) en herhalen wat we deden voordat we Vt2 en Rt2 vonden. Net nadat u de sonde in de vloeistof hebt geplaatst, wacht u een minuut of twee totdat de weerstand is verdwenen. Als je geïnteresseerd bent in de tijdrespons van de PT100, noteer dan elke 2 seconden de spanning van de seriële monitor, dan kunnen we hier een grafiek van maken en ik zal het later uitleggen. Met behulp van de twee spanningen en weerstanden kunnen we de helling als volgt berekenen:

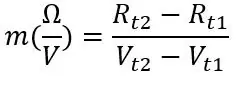
Rt1 en Rt2 zijn de weerstanden bij de twee temperaturen en hetzelfde geldt voor de spanningen Vt1 en Vt2. Uit de helling en een van de twee reeksen punten die u hebt genoteerd, kunnen we de offset berekenen:

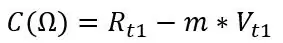
C zou dicht bij je echte Roff moeten zijn, uit mijn simulatie heb ik deze waarden berekend:

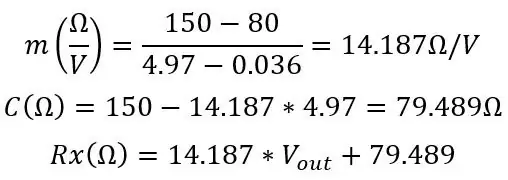
Uit deze weerstand kunnen we onze temperatuur vinden met behulp van de formule die we aan het begin hadden:

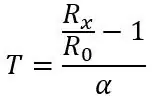
En dat is het, de code voor de Arduino staat hieronder, als je problemen hebt, laat dan gewoon een reactie achter en ik zal proberen te helpen.

Er zijn geen foto's van het circuit dat ik heb gemaakt zoals ik het een tijdje geleden heb gemaakt en heb de PT100 niet meer om opnieuw te maken en te testen, maar je moet me gewoon geloven dat het werkt. Er is niet veel over de PT100 op Instructables dat ik heb gevonden, dus daarom heb ik dit mogelijk gemaakt.

In de volgende stap zal ik het hebben over de tijdrespons van de PT100 en als je niet geïnteresseerd bent in wiskunde, laat de PT100 dan een minuut of zo rusten voordat je de meting uitvoert wanneer je een temperatuurverandering meet.

Als je geïnteresseerd bent om andere projecten te zien die ik heb gemaakt, bezoek dan mijn

Blog: Roboroblog

YouTube-kanaal: Roboro

Of kijk naar mijn andere Instructables: hier

Als de HTML knoeit met de onderstaande code, is de code bijgevoegd

* Deze code berekent de temperatuur met een PT100

* Geschreven door Roboro * Github: <a href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href="https://github.com/RonanB96/Read-Temp- Van-PT100-… <a href="https://github.com/RonanB96/Read-Temp-From-PT100-… >>>>>>>>> * Circuit: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * Blog: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * Instrustable Post: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * */ //You'll need to download this timer library from here //https://www.doctormonk.com/search?q=timer #include "Timer.h" // Define Variables float V; float temp; float Rx; // Variables to convert voltage to resistance float C = 79.489; float slope = 14.187; // Variables to convert resistance to temp float R0 = 100.0; float alpha = 0.00385; int Vin = A0; // Vin is Analog Pin A0 Timer t; // Define Timer object

void setup() {

Serial.begin(9600); // Set Baudrate at 9600 pinMode(Vin, INPUT); // Make Vin Input t.every(100, takeReading); // Take Reading Every 100ms } void loop() { t.update(); // Update Timer } void takeReading(){ // Bits to Voltage V = (analogRead(Vin)/1023.0)*5.0; // (bits/2^n-1)*Vmax // Voltage to resistance Rx = V*slope+C; //y=mx+c // Resistance to Temperature temp= (Rx/R0-1.0)/alpha; // from Rx = R0(1+alpha*X) // Uncommect to convet celsius to fehrenheit // temp = temp*1.8+32; Serial.println(temp); }

Step 6: Time Response of PT100

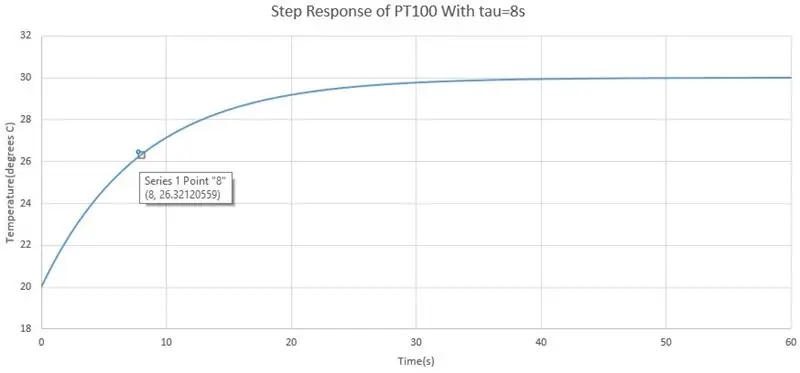
Dus ik zei dat de PT100 een langzame respons heeft, maar we kunnen op elk moment een formule krijgen voor de huidige temperatuur die door de PT100 wordt uitgelezen. De respons van de PT100 is een respons van de eerste orde die kan worden geschreven in Laplace-termen, d.w.z. overdrachtsfunctie, als:

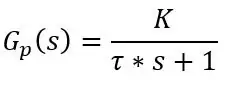
waarbij tau(τ) de tijdconstante is, K de versterking van het systeem is en s de Laplace-operator die kan worden geschreven als jω waarbij ω de frequentie is.

De tijdconstante vertelt je hoe lang het duurt voordat een systeem van de eerste orde zich op de nieuwe waarde vestigt en een vuistregel is dat 5 * tau is hoe lang het duurt om zich in de nieuwe stabiele toestand te vestigen. De versterking K vertelt u hoeveel de ingang zal worden versterkt. Met de PT100 is de winst hoeveel de weerstand verandert gedeeld door de temperatuurverandering. Door twee willekeurige waarden uit deze datasheet te kiezen, kreeg ik een winst van 0,3856 ohm/C.

Voordat ik zei dat je de spanning elke 2s kunt opnemen nadat je de sonde in de vloeistof hebt geplaatst, warm of koud, hieruit kunnen we de tijdconstante van het systeem berekenen. Eerst moet u bepalen waar het start- en eindpunt zijn, het startpunt is de spanning voordat u de sonde in de vloeistof plaatst en het eindpunt is wanneer deze is neergedaald. Trek ze vervolgens af en dat is de spanningsverandering van de stap, de test die je hebt uitgevoerd was een stapverandering die een plotselinge verandering is in de invoer naar een systeem, waarbij de stap temperatuur is. Ga nu in je grafiek naar 63,2% van de spanningsverandering en deze tijd is de tijdconstante.

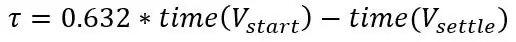
Als je die waarde in de overdrachtsfunctie stopt, heb je de formule om de frequentierespons van de systemen te beschrijven, maar dat is niet wat we nu willen, we willen de werkelijke temperatuur op tijdstip t voor een stap in temperatuur, dus we gaan om een inverse Laplace-transformatie van een stap in het systeem uit te voeren. De overdrachtsfunctie van een eerste-ordesysteem met invoer van een stap is als volgt:

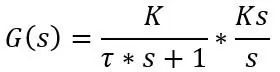
Waar Ks de stapgrootte is, d.w.z. het temperatuurverschil. Dus laten we zeggen dat de sonde zich op 20 graden C bevindt, in water van 30 graden C wordt geplaatst en de sonde een tijdconstante heeft van 8s, de overdrachtsfunctie en tijddomeinformule is als volgt:

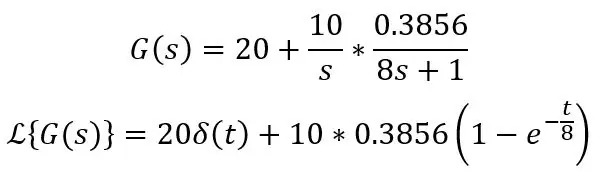
De δ(t) betekent gewoon een impuls, d.w.z. DC-offset van 20 graden C in dit geval, je kunt gewoon 20 in je vergelijkingen schrijven bij het berekenen hiervan. Dit is de standaardvergelijking voor de stap naar een eerste orde systeem:

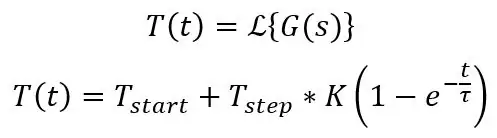
Het bovenstaande berekent de temperatuur op tijdstip t, maar dit werkt voor de spanning omdat ze evenredig zijn met elkaar, je hebt alleen de start- en eindwaarde, de tijdconstante en de stapgrootte nodig. Een website genaamd Symbolab is geweldig om te controleren of je wiskunde klopt, het kan Laplace, integratie, differentiatie en tal van andere dingen doen en het geeft je alle stappen onderweg. De inverse Laplace-transformatie hierboven is hier te vinden.