Hoge frequentie en bedrijfscyclus gelijktijdig meten met een microcontroller - Ajarnpa

2024 Auteur: John Day | [email protected]. Laatst gewijzigd: 2024-01-30 11:17

Ik weet wat je denkt: "Huh? Er zijn veel Instructables over het gebruik van microcontrollers om de signaalfrequentie te meten. Geeuw." Maar wacht, er is een nieuwigheid in deze: ik beschrijf een methode voor het meten van frequenties die veel hoger zijn dan een microcontroller (MCU) kan verdragen en de duty-cycle van het signaal - allemaal tegelijkertijd!

Het frequentiebereik van het apparaat loopt van ~43 Hz tot ~450 kHz, terwijl de duty-cycle varieert van 1% tot 99%.

Laat me het "kan dragen" -gedeelte uitleggen: een MCU meet de periode van een blokgolfsignaal, T, door de tijd tussen twee opeenvolgende overgangsgebeurtenissen te volgen. Een van de I/O-pinnen springt bijvoorbeeld van laag naar hoog. Het doet dit door het aantal pulsen van zijn eigen interne klok te tellen. Naïef zou de bovengrens voor gemeten frequenties moeten voldoen aan de Nyqvist-Shannon-steekproefstelling; d.w.z. het zou ongeveer gelijk zijn aan de helft van de klokfrequentie van de MCU. In werkelijkheid is de limiet veel, veel lager, omdat de MCU code moet uitvoeren om interrupts af te handelen, variabelen op te slaan, rekenkundige bewerkingen uit te voeren, resultaten weer te geven, enz. In mijn experimenten met een 48 MHz MCU was het minimale aantal klokcycli tussen meetbare overgangen ongeveer 106. De bovengrens van het meetbare frequentiebereik zou in dit geval dus 48.000 / 212 / 2 = 226,4 kHz zijn.

Terwijl de MCU de signaalperiode meet, kan hij ook de pulsbreedte bepalen, P: de tijd dat de signaalspanning hoog blijft. Met andere woorden, de tijd tussen de overgangen van laag naar hoog en van hoog naar laag. De duty cycle van het signaal wordt dan gedefinieerd als het volgende percentage:

Plicht = 100% * P / T

Net als in het geval van frequentie, is er een praktische limiet aan de pulsbreedte. Gebruikmakend van het bovenstaande voorbeeld, zouden 106 klokcycli de pulsbreedte beperken tot niet minder dan 2,21 microseconden. Ofwel maar liefst 50% bij 226,4 kHz.

Een van de manieren om de bovenste frequentielimiet van blokgolfsignalen te verhogen, is de toepassing van digitale verdelers die gebruik maken van flip-flops. Het delen van de ingangsfrequentie door n zou het meetbare bovenbereik n maal verlengen. Dit is geweldig nieuws, digitale verdelers hebben één fundamentele fout: verdeeld signaal verliest de informatie over de pulsbreedte (en duty cycle)! Vanwege de manier waarop de verdelers werken, heeft hun output altijd 50% inschakelduur. Jammer…

Op de volgende pagina's zal ik echter laten zien hoe ik de frequentie digitaal kan verdelen en de oorspronkelijke pulsbreedte kan behouden, waardoor ik signalen kan meten die ver buiten de limieten liggen die worden opgelegd door direct tellen.

Stap 1: Digitale frequentieverdeling

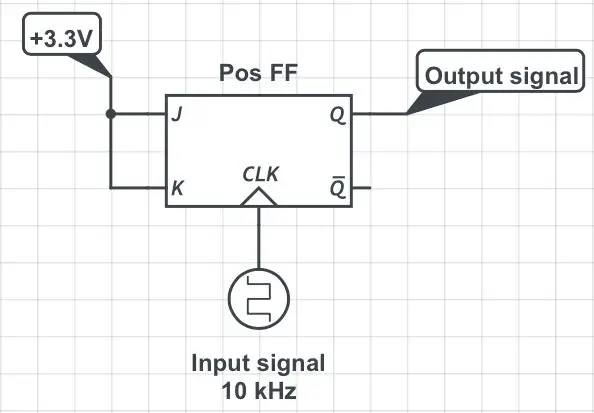
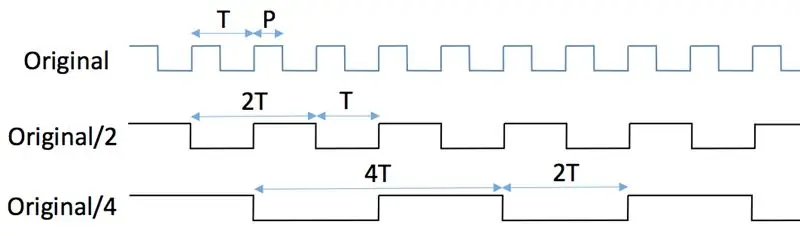
Traditionele digitale frequentiedelers gebruiken flip-flops; deze tutorial legt mooi de principes uit hoe je verdelers kunt maken met behulp van standaard JK-flip-flops. Dit lost het probleem op van te hoge ingangsfrequenties voor de MCU, maar heeft één groot nadeel: verdeeld signaal heeft een duty cycle van 50%, ongeacht de taak van het ingangssignaal! Kijk naar de eerste twee figuren om te zien waarom dit het geval is. Het originele signaal met periode T en pulsbreedte P wordt ingevoerd in de klokpen van een JK-flip-flop terwijl de J- en K-pennen altijd hoog worden gehouden (eerste cijfer). Er wordt overal uitgegaan van logica van 3,3 V. Laten we aannemen dat de flip-flop wordt geactiveerd door de positieve (d.w.z. stijgende) flank van de klok. Onder deze omstandigheden vinden veranderingen in de toestand van de uitgangspen (individuele "flips" en "flops") plaats telkens wanneer de klokpen van laag naar hoog gaat. De overgang van hoog naar laag van de klok (d.w.z. de negatieve flank) wordt volledig genegeerd. Zie de tweede figuur. De uitgangspen, Q, zendt een signaal uit waarvan de periode twee keer zo lang is als de oorspronkelijke periode, d.w.z. de frequentie wordt gehalveerd. De pulsbreedte van de uitgang is altijd gelijk aan T. Bijgevolg gaat de oorspronkelijke pulsbreedte, P, verloren.

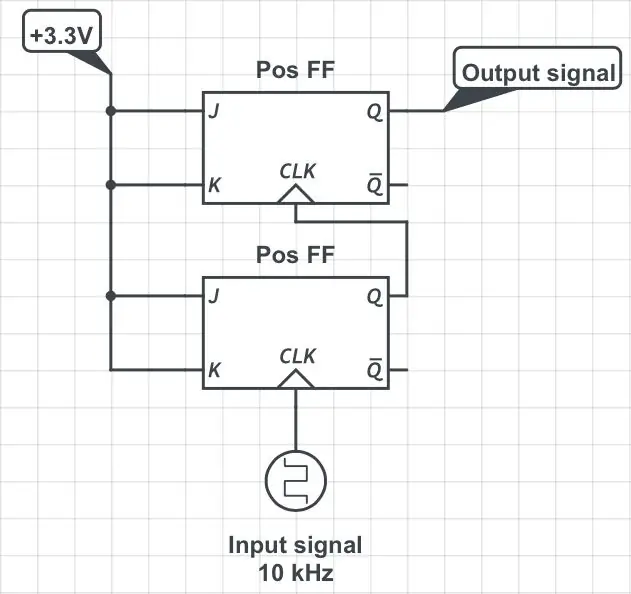
Als u nog een JK-flip-flop toevoegt in een configuratie die wordt weergegeven in de derde figuur, wordt de oorspronkelijke frequentie gedeeld door 4. Als u meer flip-flops op dezelfde sequentiële manier toevoegt, wordt de frequentie gedeeld door volgende machten van 2: 8, 16, 32, enz.

Probleem: hoe verdeel je de frequentie van een blokgolf met behoud van de pulsbreedte?

Het idee is om op de juiste manier een JK-flip-flop met negatieve edge toe te voegen aan de mix. Laten we het "Neg FF" noemen; zie vierde figuur. Hier betekent "goed" dat de J- en K-pinnen van de nieuwe flip-flop zijn gekoppeld aan respectievelijk de Q- en Qbar-uitgangspinnen van de deler-door-4 ("Pos FF") geïllustreerd in de vorige afbeelding. (Hier is "bar" de horizontale balk boven het Q-symbool dat logische ontkenning aangeeft.) Om te zien wat dit oplevert, kijk eens naar de functietabel van de "Neg FF" in de vijfde figuur: Neg's uitgangspinnen, Q en Qbar, weerspiegelen de toestand van de invoerpinnen, respectievelijk J en K. Wat betekent dat ze de toestand van de Q en Qbar van de Pos weerspiegelen. Maar de flip-flop-actie van de Neg moet wachten op de negatieve flank van het oorspronkelijke signaal, dat op tijd P na de positieve flank arriveert. Aha!

De resulterende golfvormen worden geïllustreerd in de zesde figuur. "Pos Q" voert een signaal uit op 1/4e frequentie, "Pos Qbar" is het inverse, "Neg Q" volgt "Pos Q" verschoven met pulsbreedte P, en "Neg Qbar" is het omgekeerde. U kunt controleren of de logische EN van "Pos Qbar" en "Neg Q" een pulsreeks produceert die wordt gekenmerkt door de oorspronkelijke pulsbreedte P en 1/4e van de frequentie. Bingo!

In eerste instantie gebruikte ik precies dit uitgangssignaal om de MCU te voeden. Het bleek echter problematisch te zijn voor zeer korte pulsbreedtes vanwege de in de inleiding genoemde beperking van 106 cycli van de MCU. Ik heb dit kleine probleem opgelost door in plaats daarvan een andere uitvoer te kiezen: "Pos Qbar" EN "Neg Qbar". Eén blik op de golfvormen zou u ervan moeten overtuigen dat de pulsbreedte van deze specifieke golfvorm, P', varieert tussen T en 2T in plaats van (0, T) voor P. De P kan gemakkelijk worden hersteld van P' door:

P = 2T - P'

Stap 2: Aanbevolen hardware

Ik hou echt van de relatieve nieuwkomer voor elektronische hobbyisten: Atmel SAM D21 MCU's gebaseerd op de 32-bit ARM Cortex M0+ processor die werkt op 48 MHz kloksnelheid, veel hoger dan de oudere Atmels. Voor dit project kocht ik:

• ItsyBitsy M0 Express MCU-bord van Adafruit
• Ik had toevallig een oplaadbare LiPo-batterij van Adafruit
• Monochroom 128x32 SPI OLED-scherm (je raadt het al: Adafruit)
• Dual positive-edge-getriggerde JK flip-flop SN74HC109 van Texas Instruments
• Dubbele negatieve-edge-getriggerde JK flip-flop SN74HC112 van Texas Instruments
• Viervoudige EN-poort CD74AC08E van Texas Instruments
• Viervoudige OK-poort CD74AC32E van Texas Instruments

Stap 3: Het circuit

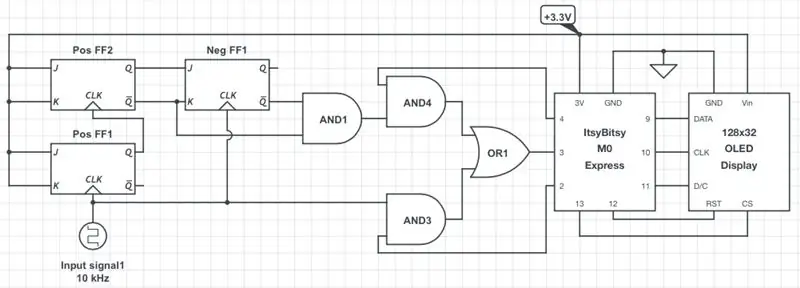
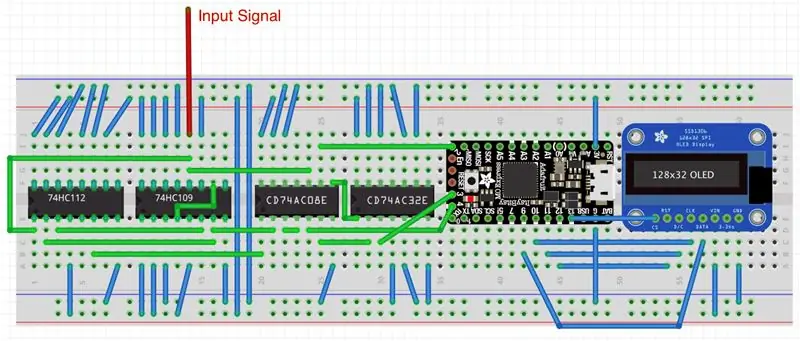
De eerste afbeelding toont een vereenvoudigd schema van de frequentie-/dienstmeter. Overal wordt uitgegaan van de 3.3 V CMOS-logica. Bijgevolg moet de amplitude van de ingangsblokgolf tussen de corresponderende V_IH niveau (d.w.z. 2 V) en 3,3 V. Zo niet, dan moet u het overeenkomstig omhoog of omlaag schalen. In de meeste gevallen zou een eenvoudige spanningsdeler voldoende zijn. Als je je versie van de meter op een ander logisch niveau wilt ontwerpen, dan moet je een andere microcontroller (MCU), batterij en een display gebruiken die op het gewenste niveau werken. De logische poorten en flip-flops die in dit project worden gebruikt, werken met logische niveaus ergens tussen 2 V en 6 V en zouden in de meeste gevallen in orde moeten zijn.

Zoals getoond, gebruikt de ItsyBitsy MCU pinnen 9-13 om te communiceren met het scherm via het software SPI-protocol. De 3V-pin levert stroom aan het hele circuit. Digitale ingangspen 3 accepteert het geanalyseerde signaal, terwijl pennen 2 en 4 de signaalbron besturen: ofwel direct signaal dat door poort AND3 (lage ingangsfrequenties) komt, of signaal gedeeld door 4 door poort AND4 (hoge ingangsfrequenties) zoals beschreven in stap 2 De code, die in de volgende stap wordt besproken, detecteert automatisch het inkomende frequentiebereik en schakelt de signaalbron op de juiste manier.

Het schema toont niet de ware complexiteit van digitale chipverbindingen. De tweede afbeelding laat zien hoe het project eruit zou zien op een breadboard. Het ingangssignaal komt via een rode draad naar de 2CLK-pin van de flip-flop met dubbele positieve rand. LET OP: Normaal gesproken moeten alle J- en K-pinnen van deze flip-flop hoog worden gehouden, maar SN74HC109 heeft in plaats daarvan de Kbar-pin - een omgekeerde K-pin. Deze pin moet dus geaard zijn! De eerste flip-flop met negatieve rand in SN74HC112 heeft zijn 1K- en 1J-pin verbonden met de 1Q- en 1Qbar-pinnen van SN74HC109. De tweede flip-flop in SN74HC112 is ongebruikt en de ingangspinnen (2K, 2J, 2CLRbar) zijn geaard. Alle andere extra pinnen PREbar (preset) en CLRbar (clear) in alle flip-flops moeten op logisch hoog worden aangesloten. Ongebruikte klok- en uitgangspinnen zijn niet aangesloten. Evenzo zijn ongebruikte ingangspinnen in alle poorten geaard, terwijl ongebruikte uitgangspinnen niet zijn aangesloten. Zoals ik in mijn "Invisible Killer of the Phone Ring" heb besproken, elimineert het aarden van ongebruikte ingangspinnen van logische chips willekeurige oscillaties en bespaart het batterijvermogen.

Stap 4: De code en het meten van lage frequenties

Uiteraard gebeurt alle actie in de onderstaande code. Wanneer de ingang die binnenkomt op pin 3 overschakelt van digitaal laag naar hoog, begint de MCU pulsen te tellen van zijn interne 48 MHz-klok. Het noteert het moment van de overgang van hoog naar laag en telt verder tot de volgende laag naar hoog omschakeling, waarna het hele proces opnieuw wordt gestart. De eerste telling vertegenwoordigt de pulsbreedte, terwijl de volledige telling de periode van het signaal vertegenwoordigt. En dat is het hele geheim.

De CPU noteert deze overgangen via hardware-interrupts. De SAMD21 heeft verschillende klokken; mijn code gebruikt TC3 een. In eerste instantie ben ik begonnen met het lezen van de datasheet van de M0 die veel moeite kostte bij het coderen van de interrupt-handler, maar al snel heb ik een zeer gerelateerde code ontdekt in de Arduino Forum-berichten van gebruikers electro_95, MartinL en Rucus wiens bijdrage is naar behoren erkend. Ik heb hun gecombineerde code in de mijne opgenomen en aangepast; scheelt me veel tijd!

Zoals ik eerder al zei, wordt de signaalresolutie beperkt door ~106 CPU-cycli om code tussen interrupts uit te voeren. Digitale verdeling met behoud van pulsbreedte zorgt voor hoge frequenties. Lage frequenties daarentegen vormen een andere uitdaging: aangezien de TC3-klokteller 16 bits lang is, loopt hij over na het overschrijden van de limiet van 65, 536 tellingen. Men kan met deze situatie omgaan door een overflow-interrupt toe te voegen, maar een andere oplossing kiezen: TC3 kan een voorgeschaalde (d.w.z. software-gedeelde) CPU-klok gebruiken in plaats van de hardware 48 MHz. Dus als de periode van het signaal de overlooplimiet nadert, kan de code TC3 instrueren om 24 MHz-tellingen te gebruiken voor de volgende periode en, voila, de teller zakt onder 32, 768 tellingen. Voor nog lagere frequenties kan de TC3 worden geïnstrueerd om 12 MHz-pulsen te tellen, enz. De juiste prescaler wordt automatisch bepaald op basis van de frequentie van het signaal, met hysterese, om de TC3-teller binnen de overlooplimiet te houden. Als gevolg hiervan is de onderkant van het bereik van het apparaat ongeveer 43 Hz.

U bent van harte welkom om de code te forken en te gebruiken in uw project, maar vermeld de bron bij het publiceren van resultaten.

Link naar de code.