Het voorschrift van uw oogbol in de gaten houden: een BME60B-project - Ajarnpa

2025 Auteur: John Day | [email protected]. Laatst gewijzigd: 2025-01-23 15:01

Door: Hannah Silos, Sang Hee Kim, Thomas Vazquez, Patrick Viste

Vergroting is een van de belangrijkste kenmerken die aanwezig zijn voor leesbrillen, die worden geclassificeerd op basis van hun voorschrift van dioptrie. Volgens de Michigan Technology University is een dioptrie een brandpuntsafstand van de lens, meestal gemeten in mm, in meters (Michigan Technology University). Omdat een leesbril bolle lenzen heeft, zou de brandpuntsafstand positief zijn, waardoor de dioptrie ook positief zou zijn (HyperPhysics). De brandpuntsafstand neemt toe naarmate de afstand tussen het object verder van de eigenlijke lens komt, en dit leidt ertoe dat de dioptrieën afnemen omdat ze omgekeerd evenredig zijn. Daarom zou het hebben van een leesbril met extra dioptrieën de lens helpen om in het zicht in te zoomen, zodat het lijkt alsof de brandpuntsafstand kleiner is door de waarde van de dioptrieën te vergroten.

De gepresenteerde code zal worden gebruikt om de dioptrie van een lens met een onbekende sterkte te voorspellen. Er worden twee inputs gebruikt om het recept te berekenen: een foto van de gecontroleerde achtergrond zonder gebruik van lenzen, en een andere foto van dezelfde achtergrond maar door de lens naar keuze. Het programma meet de vervorming tussen deze twee foto's. Van daaruit kunnen we de dioptrie van de lens schatten en een resultaat produceren dat de gebruiker kan bekijken.

Voor deze Instructable heb je nodig:

• Een zwart-wit dambordpatroon gedrukt op een vel papier van 11x8.5 inch
• Een camera met de mogelijkheid om de focus te vergrendelen
• Een statief of iets dergelijks om de camera vast te zetten
• Diverse voorschriften voor leesbrillen
• MATLAB

Stap 1: Foto's maken

Om de vergroting van een lens te berekenen, moet je deze kunnen vergelijken met de werkelijke grootte van het object. Voor dit project zullen we een vergroot beeld vergelijken met een controlebeeld.

De eerste stap is dus om twee foto's van hetzelfde beeld te maken - de eerste door alleen de camera en de tweede door de lens van de leesbril die u wilt testen.

Je maakt een foto van een zwart-wit dambord van 8,5 x 11 inch met een raster van 1 inch. Stel uw camera 11 inch uit de buurt van het dambord. Vergrendel de focus op het dambord voordat u de foto's maakt.

Maak een foto van het dambord zonder de leesbril. Plaats vervolgens zonder iets te bewegen de leesbril voor de camera en maak de tweede foto.

Zorg ervoor dat de positie van uw camera niet verschuift tussen opnamen. Het enige dat tussen de twee foto's zou moeten veranderen, is de aanwezigheid van de brillens voor de camera.

Als u klaar bent met de foto's, uploadt u ze naar uw computer.

Stap 2: Laad de afbeeldingen in MATLAB

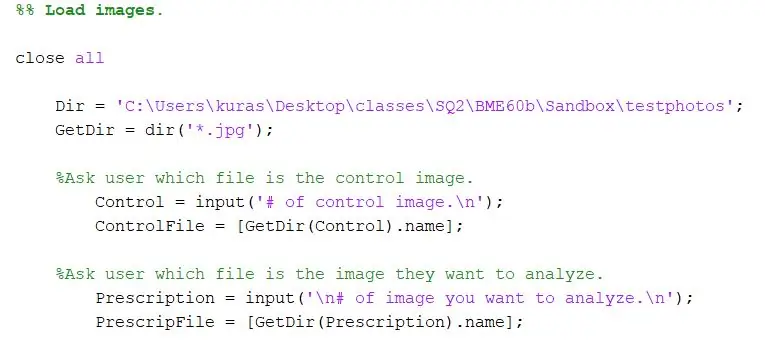
Open een nieuw schrift.

Geef eerst de map op waar de foto's zijn opgeslagen. Gebruik vervolgens de dir-functie om.jpg-afbeeldingen uit te pakken (of welk bestandstype uw afbeelding ook is).

Dir = 'C:\Users\kuras\Desktop\classes\SQ2\BME60b\Sandbox\testphotos'; GetDir = dir('*.jpg');

Voor ons project wilden we de gebruiker van het programma vragen welke bestanden ze wilden vergelijken. De eerste sectie vraagt de gebruiker om het controlebeeld te specificeren, en het tweede vraagt de gebruiker om het testbeeld te specificeren.

• %Vraag de gebruiker welk bestand het controlebeeld is.
• Control = input('# van controleafbeelding.\n');
• ControlFile = [GetDir(Control).naam]
• %Vraag de gebruiker welk bestand de afbeelding is die ze willen analyseren.
• ChooseFile = input('\n# van de afbeelding die u wilt analyseren.\n');
• PrescripFile = [GetDir(ChooseFile).naam];

Stap 3: Beeldanalyse

Een gekleurde afbeelding in MATLAB heeft de grootte MxNx3, terwijl een afbeelding in grijswaarden MxN heeft. Dit betekent dat het sneller is om een afbeelding in grijswaarden te verbeteren/bewerken omdat er minder gegevens zijn om bij te houden. Gebruik rgb2gray om de afbeelding naar grijswaarden te converteren. (De imrotate-functie werd gebruikt omdat onze foto's horizontaal kwamen - deze regel code kan al dan niet nodig zijn in uw versie.)

• %converteren naar grijswaarden en roteren
• I = imread (ControlFile);
• ik = rgb2gray(I);
• I = imroteren (I, 90);

Geef vervolgens de afbeelding weer. De subplot-functie wordt gebruikt zodat het testbeeld in latere stappen naast de besturing kan staan.

• %Scherm
• Figuur 1);
• subplot(1, 2, 1)
• imshow(ik);
• titel (ControlFile);

Gebruik imcrop om de gebruiker te vragen het dambord uit de volledige afbeelding bij te snijden. De volgende code toont ook een berichtvenster om instructies aan de gebruiker te geven.

• % dambord uitsnijden voor analyse
• waitfor(msgbox({'Gebruik het dradenkruis om het dambord uit te snijden.', 'Dubbelklik vervolgens op het interessegebied.'}));
• I_crop = imcrop(I);

Gebruik imbinarize om de afbeelding te binariseren.

I_binary = imbinariseren (I_crop);

Stap 4: Bereken de breedte van de witte vierkanten op het dambord

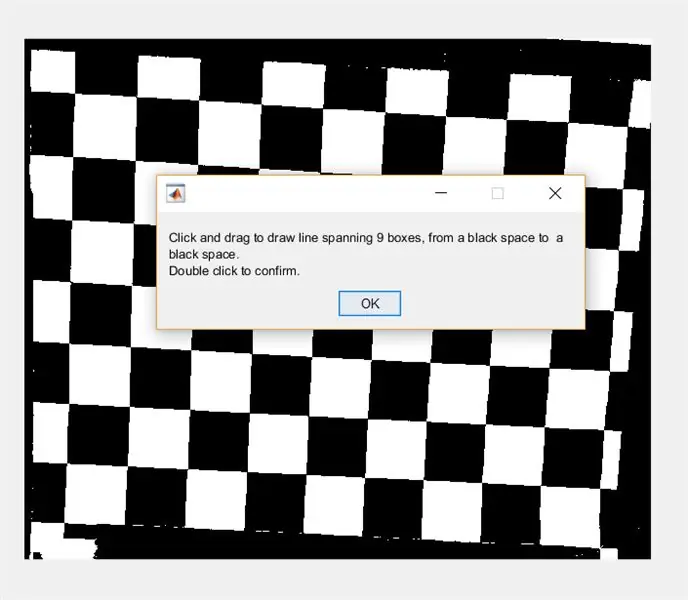
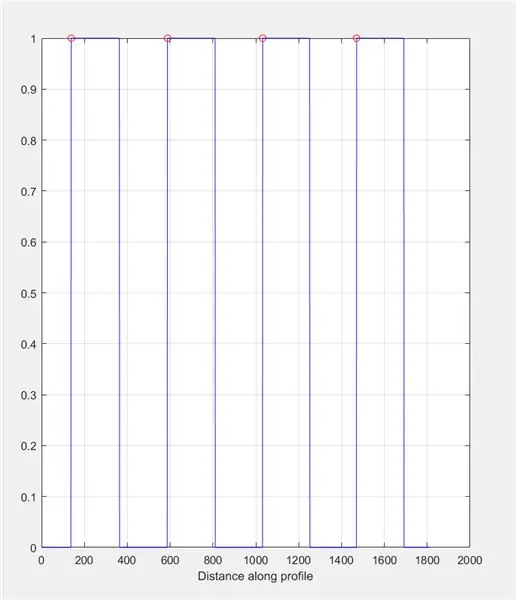
Vraag de gebruiker vervolgens om een lijn over de afbeelding te tekenen met imline. Deze lijn moet horizontaal over het dambord lopen. Het moet beginnen en eindigen op een zwart vierkant (het maakt niet uit waar) - dit is omdat we de breedte van de witte vierkanten zullen meten, niet de zwarte.

• %teken lijn
• Figuur 1)
• subplot(1, 2, 1)
• imshow(I_binair);
• waitfor(msgbox({'Klik en sleep om een lijn te tekenen die 9 vakken overspant, van een zwarte ruimte naar een zwarte ruimte.', 'Dubbelklik om te bevestigen.'}));
• lijn = imline;
• positie = wacht(lijn);
• eindpunten = line.getPosition;

Extraheer de X- en Y-coodinaten voor de eindpunten van de getekende lijn.

• X = eindpunten(:, 1)
• Y = eindpunten(:, 2);

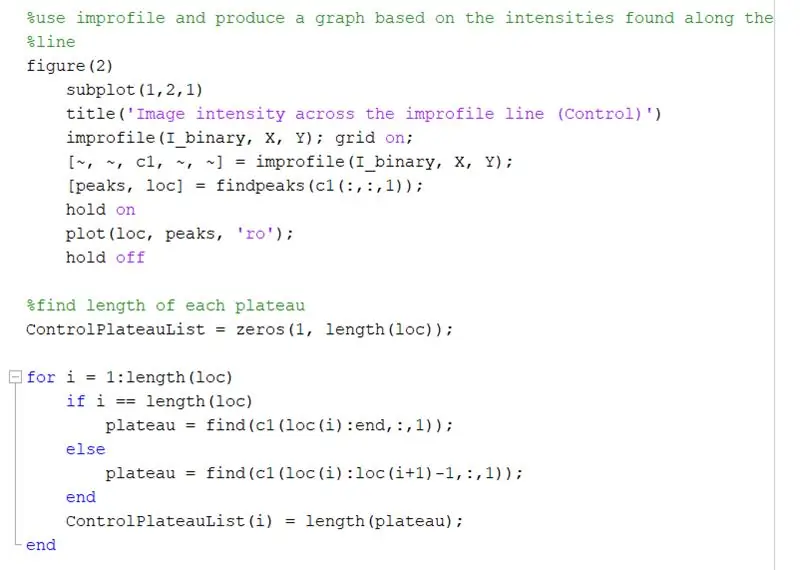
Gebruik improfile om een grafiek te maken op basis van de intensiteiten die langs de getekende lijn worden gevonden. Dit moet lijken op een blokgolf van 0 (zwart) tot 1 (wit). Bereken ook de toppen en hun locaties.

• Figuur 2)
• subplot(1, 2, 1)
• title('Beeldintensiteit over de improfiellijn (Controle)')
• improfile (I_binair, X, Y); rooster aan;
• [~, ~, c1, ~, ~] = improfile(I_binary, X, Y);
• [pieken, loc] = vindpieken(c1(:,:, 1));
• vasthouden
• plot(loc, pieken, 'ro');
• wacht af

Zoek de lengte van elk plateau op de improfile-grafiek met behulp van een for-lus. Voer de for-lus uit voor hetzelfde aantal pieken als in de improfile-grafiek. Om de lengte van elk plateau te berekenen, gebruikt u de functie 'vinden' om alle locaties te vinden waar er een '1' is in plaats van een '0' intensiteitswaarde. Bereken vervolgens de lengte van die array om de totale lengte van het plateau te krijgen, die gelijk moet zijn aan de breedte van een wit vierkant in pixels. ControlPlateauList = zeros(1, length(loc));

voor i = 1: lengte (loc)

als ik == lengte(loc)

plateau = find(c1(loc(i):end,:, 1));

anders

plateau = find(c1(loc(i):loc(i+1)-1,:, 1));

einde

ControlPlateauList(i) = lengte(plateau);

einde

Stap 5: Herhaal stap 3 en 4 voor de testafbeelding

*Opmerking: wanneer u de niet-profiellijn op de testafbeelding tekent, moet u ervoor zorgen dat u deze over de vierkanten trekt die overeenkomen met de lijn die u op de controleafbeelding hebt getekend.

Stap 6: Bereken de vergroting van de lens

De vergrote metingen worden berekend door het gemiddelde van de lengte van het plateau, dat werd berekend in stap 5, te delen door het gemiddelde van de lengte van het controleplateau, dat werd berekend in stap 4. Dit wordt berekend op 1,0884.

vergroting = mean(plateauList)/mean(ControlPlateauList);

Stap 7: R-kwadraat vinden en het recept van de gebruiker via interpolatie

De code gebruiken:

• md1 = fitlm (GivenPrescription, MagArray);
• Rkwadraat = md1. Rkwadraat. Gewone;

We kunnen de R-kwadraatwaarde van de grafiek GivenPresciption (onze lenzen gegeven waarden) versus MagArray (een reeks van de vergrotingsmetingsverhoudingen die we eerder hebben berekend) vinden. Door een voldoende hoge R-kwadraatwaarde te hebben, kan worden afgeleid dat er een voldoende sterke correlatie is om het gebruik van deze methode te rechtvaardigen. Voor dit specifieke geval was de R-kwadraatwaarde 0,9912, wat een sterke correlatie suggereert en daarom gerechtvaardigd is om deze methode in analyse te gebruiken.

De functie gebruiken:

Prescription = interp1(MagArray, GivenPrescription, vergroting, 'lineair');

We kunnen de corresponderende receptwaarde (op de x-as) van onze vergrotingsverhouding (een waarde op de y-as) interpoleren en vinden wat het recept van de gebruiker is.

Het interpoleren van gegevens is belangrijk om deze methode te laten werken, omdat het ons in staat stelt om aannames te doen over informatie die we niet hebben, op basis van de informatie die we wel hebben. Hoewel een lijn met de beste pasvorm technisch gezien een sterkere kandidaat zou zijn voor deze veronderstelling, heeft het creëren van grenzen om het aantal outputs te verminderen hetzelfde effect als brillen op sterkte hoe dan ook in toenemende uniforme waarden. Dit wordt uitgelegd in latere stappen.

Stap 8: Het recept van de gebruiker in een grafiek weergeven

Met behulp van de volgende code:

• figuur;
• plot (GivenPrescription, MagArray, '-g')
• vasthouden
• plot (recept, vergroting, 'bp')
• wacht af
• rooster
• legend('Gegevens', 'Geïnterpoleerde punten', 'Locatie', 'NW')

We kunnen een grafiek plotten die de vergrotingsratio's versus het gegeven recept weergeeft met een groene lijn en de gevonden gegevens van onze berekende vergroting versus ons geïnterpoleerde recept met een blauwe ster. Vervolgens labelt de legenda de titel, x-as en y-as en plaatst de legenda in de linkerbovenhoek.

Stap 9: Beperk uw recept

De volgende code wordt gebruikt om de afronding voor het recept te maken:

• als recept <= 1.125

  BerekendPrescription = '1.0';

• elseif Recept <= 1.375

  BerekendPrescription = '1,25';

• elseif Recept <= 1.625

  BerekendPrescription = '1,5';

• elseif Recept <= 1.875

  BerekendPrescription = '1.75';

• elseif Recept <= 2.25

  BerekendPrescription = '2.0';

• elseif Recept <= 2.625

  BerekendPrescription = '2,5';

• elseif Recept <= 3

  BerekendPrescription = '2.75';

• elseif Recept <= 3.375

  BerekendPrescription = '3.25';

• anders

  BerekendPrescription = 'onbekend';

• einde

Het recept dat door interpolatie wordt gevonden, komt niet noodzakelijk overeen met het werkelijke recept - dit komt omdat er altijd kleine variaties in het analyseren van de foto zullen zijn als gevolg van menselijke fouten. We hebben deze stap dus nodig om het eigenlijke recept te classificeren.

De voorschriften die worden gegeven beginnen meestal vanaf 1,0 dioptrie en nemen toe met 0,25 in hun voorschriften, dus na het berekenen van het recept willen we het recept bepalen dat het beste past bij wat de gebruiker nodig heeft. Na het berekenen van het recept, lopen we het door de gegeven If-instructies om de waarde te controleren en te bepalen welk recept nodig is. Alles kleiner dan of gelijk aan 1,125, dan is het recept 1,0. Alles kleiner dan of gelijk aan 1,375, is het recept 1,25. Alles kleiner dan of gelijk aan 1,625, is het recept 1,5. Alles kleiner dan of gelijk aan 1,845, is het recept 1,75. Enzovoort.

We laten de waarden toenemen omdat we controleren of de waarden kleiner zijn dan. Als we de waarden zouden verlagen, zou het eerste if-statement altijd het eerste if-statement lezen. Als het recept het kleinste is, willen we dat het het meteen als het kleinste herkent, dus daarom zijn we begonnen met de kleinste waarde. Alles hoger dan de hoogste waarde betekent dat het recept niet binnen het bereik van onze gegevens ligt, dus het geeft de "Onbekende" tekenreekswaarde.