Inhoudsopgave:
- Auteur John Day day@howwhatproduce.com.
- Public 2024-01-30 11:15.
- Laatst gewijzigd 2025-01-23 15:01.

In deze instructable zal ik uitleggen wat een lopend gemiddelde is en waarom je er om zou moeten geven, en je laten zien hoe het moet worden geïmplementeerd voor maximale rekenefficiëntie (maak je geen zorgen over complexiteit, het is heel eenvoudig te begrijpen en ik zal bieden ook een eenvoudig te gebruiken bibliotheek voor uw arduino-projecten:)
Lopend gemiddelde, ook wel voortschrijdend gemiddelde, voortschrijdend gemiddelde of lopend gemiddelde genoemd, is een term die wordt gebruikt voor het beschrijven van de gemiddelde waarde van de laatste N-waarden in gegevensreeksen. Het kan worden berekend als een normaal gemiddelde of u kunt een truc gebruiken om ervoor te zorgen dat het een minimale impact heeft op de prestaties van uw code.
Stap 1: Use Case: ADC-metingen gladstrijken

Arduino heeft een fatsoenlijke 10 bit ADC met heel weinig ruis. Bij het meten van waarde op een sensor zoals een potentiometer, fotoweerstand of andere componenten met veel ruis, is het moeilijk te vertrouwen dat de meting correct is.
Een oplossing is om elke keer dat u uw sensor wilt uitlezen meerdere metingen te doen en deze uit te middelen. In sommige gevallen is dit een haalbare oplossing, maar niet altijd. Als u ADC 1000 keer per seconde zou willen lezen, zou u 10 000 moeten hebben als u gemiddeld 10 metingen zou doen. Een enorme verspilling van rekentijd.
Mijn voorgestelde oplossing is om 1000 keer per seconde metingen uit te voeren, het lopende gemiddelde elke keer bij te werken en het als huidige waarde te gebruiken. Deze methode introduceert enige latentie, maar vermindert de computationele complexiteit van uw toepassing, waardoor u veel meer tijd heeft voor aanvullende verwerking.
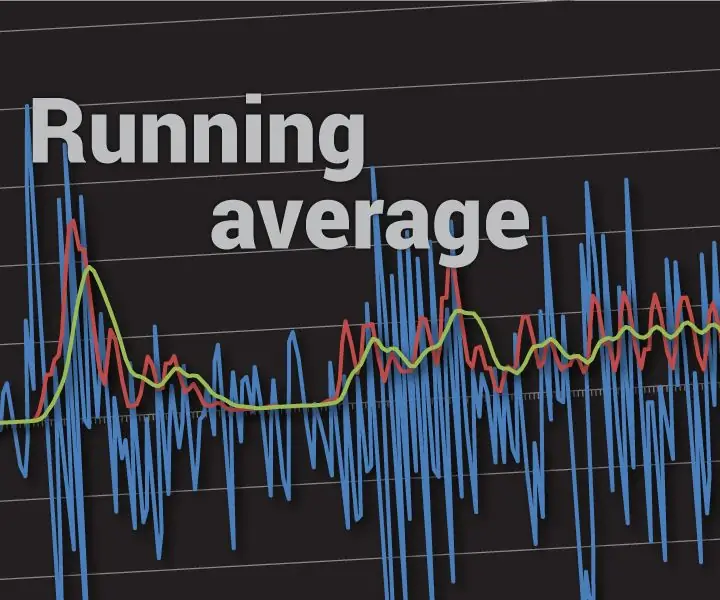
In bovenstaande afbeelding gebruikte ik het lopende gemiddelde van de laatste 32 metingen. U zult zien dat deze methode niet 100% storingsbestendig is, maar de nauwkeurigheid aanzienlijk verbetert (het is niet slechter dan gemiddeld 32 monsters per keer). Als je elke keer gemiddeld 32 metingen zou willen berekenen, zou dat op Arduino UNO alleen al voor metingen meer dan 0,25 ms duren!
Stap 2: Use Case: DC-component van microfoonsignaal meten



Arduino kan spanningen meten tussen 0 en Vcc (normaal 5 V). Het audiosignaal is volledig AC en als je het op een microcontroller wilt meten, moet je het rond 1/2 Vcc instellen. In een Arduino UNO-project zou dat ongeveer 2,5 V (DC) + audiosignaal (AC) betekenen. Bij gebruik van 10 bit ADC en 5 V voeding, moet 2,5 V bias gelijk zijn aan de meting van 512. Dus om een AC-waarde van het signaal te krijgen, moet 512 worden afgetrokken van de ADC-meting en dat is het, toch?
In een ideale wereld zou dat waar zijn. Helaas is het echte leven ingewikkelder en neigt onze signaalbias af te drijven. Heel gebruikelijk is 50 Hz ruis (60 Hz als u in de VS woont) van het elektriciteitsnet. Meestal is het niet al te problematisch, maar het is goed om te weten dat het bestaat. Meer problematisch is lineaire drift door verhitting van componenten. U stelt de DC-offsetcorrectie zorgvuldig in bij het starten en deze drijft langzaam weg terwijl uw toepassing draait.
Ik zal dit probleem illustreren met een (muziek)beatdetector. Je stelt je bias-verwijdering in en beats zijn duidelijk (afbeelding 2). Na enige tijd zijn DC-biasbewegingen en beats nauwelijks waarneembaar voor de microcontroller (afbeelding 3). Het algoritme voor het detecteren van beats zal in een toekomstig instructable diepgaand worden onderzocht, omdat dit het bestek van dit artikel overschrijdt.
Gelukkig is er een manier om constant de DC-offset van audio te blijven berekenen. Het zal geen verrassing zijn dat het lopende gemiddelde, het onderwerp van deze instructable, een oplossing biedt.
We weten dat de gemiddelde waarde van elk AC-signaal 0 is. Met behulp van deze kennis kunnen we afleiden dat de gemiddelde waarde van het AC + DC-signaal de DC-bias is. Om het te verwijderen, kunnen we een lopend gemiddelde nemen van de laatste paar waarden en dit aftrekken van de huidige ADC-waarde. Houd er rekening mee dat u een lang genoeg lopend gemiddelde moet gebruiken. Voor audio zou een tiende van een seconde (aantal samples hangt af van je samplefrequentie) voldoende moeten zijn, maar weet dat langere gemiddelden beter werken. In de eerste afbeelding ziet u een voorbeeld van een echte DC-biasberekening met een lopend gemiddelde met 64 elementen bij een samplefrequentie van 1 kHz (minder dan ik heb aanbevolen, maar het werkt nog steeds).
Stap 3: Berekening

Je kunt je het lopende gemiddelde voorstellen als het gemiddelde gewicht van mensen in de wachtkamer van de dokter. Dokter is klaar met het onderzoeken van een patiënt en tegelijkertijd loopt een nieuwe de wachtkamer binnen.
Om het gemiddelde gewicht van alle wachtende patiënten in de wachtkamer te achterhalen, zou de verpleegster elke patiënt naar hun gewicht kunnen vragen, die getallen optellen en delen door het aantal patiënten. Elke keer dat de arts een nieuwe patiënt accepteert, herhaalt de verpleegster het hele proces.
Je denkt misschien: "Dit klinkt niet al te efficiënt… Er moet een betere manier zijn om dit te doen." En je zou gelijk hebben.
Om dit proces te optimaliseren, zou de verpleegkundige het totale gewicht van de huidige groep patiënten kunnen bijhouden. Zodra de dokter een nieuwe patiënt belt, zou de verpleegster hem vragen naar zijn gewicht en dit aftrekken van het groepstotaal en hem laten gaan. De verpleegster zou dan de patiënt die net de wachtkamer binnenkwam vragen naar zijn gewicht en dit optellen bij het totaal. Het gemiddelde gewicht van de patiënten na elke dienst zou de som zijn van de gewichten gedeeld door het aantal patiënten (ja, hetzelfde als voorheen, maar nu vroeg de verpleegster slechts twee mensen naar hun gewicht in plaats van allemaal). Ik realiseer me dat deze paragraaf misschien een beetje verwarrend was, dus zie bovenstaande afbeelding voor meer duidelijkheid (of stel vragen in opmerkingen).
Maar zelfs als je de laatste alinea niet verwarrend vond, heb je misschien vragen zoals wat er in het begin in de accumulator zou moeten staan, hoe zet ik wat ik net heb gelezen in een echte C-code? Dat komt aan de orde in de volgende stap, waar je ook mijn broncode krijgt.
Stap 4: De code

Om het lopend gemiddelde te berekenen, hebt u eerst een manier nodig om de laatste N-waarden op te slaan. je zou een array met N-elementen kunnen hebben en de hele inhoud één plaats kunnen verplaatsen elke keer dat je een element toevoegt (doe dit alsjeblieft niet), of je zou een oud element kunnen overschrijven en de aanwijzer aanpassen naar het volgende element dat moet worden weggegooid (doe dit alstublieft:)
Accumulator zou moeten beginnen geïnitialiseerd op 0, hetzelfde geldt voor alle elementen in de vertragingslijn. In andere gevallen zal uw lopende gemiddelde altijd verkeerd zijn. U zult zien dat delayLine_init zorgt voor het initialiseren van de vertragingslijn, u dient zelf voor de accumulator te zorgen.
het toevoegen van een element aan de vertragingslijn is net zo eenvoudig als het verlagen van de index van het nieuwste element met 1, en ervoor zorgen dat het niet naar de kant van de vertragingslijnarray wijst. na het verlagen van de index wanneer deze 0 is, zal het rondlopen naar 255 (omdat het een 8-bits geheel getal zonder teken is). Modulo (%) operator met de grootte van delay line array zorgt ervoor dat de index naar een geldig element verwijst.
Het berekenen van een lopend gemiddelde zou gemakkelijk te begrijpen moeten zijn als je mijn analogie in de vorige stap hebt gevolgd. Trek het oudste element af van de accumulator, voeg de nieuwste waarde toe aan de accumulator, duw de nieuwste waarde naar de vertragingslijn, retourneer de accumulator gedeeld door het aantal elementen.
Makkelijk, toch?
Experimenteer gerust met het gebruik van de bijgevoegde code om beter te begrijpen hoe dit allemaal werkt. Zoals het er nu uitziet, leest Arduino de analoge waarde op analoge pin A0 en drukt "[ADC-waarde], [lopend gemiddelde]" op de seriële poort af met een baudrate van 115200. Als je de seriële plotter van Arduino op de juiste baudrate opent, zie je twee regels: ADC-waarde (blauw) en afgevlakte waarde (rood).
Stap 5: Extra's

Er zijn een paar dingen die u niet per se hoeft te weten om het lopend gemiddelde in uw project te gebruiken, maar het kan geen kwaad om te weten.
vertraging: ik zal beginnen met praten over de illustratie van deze stap. U zult merken dat het gemiddelde van meer elementen een grotere vertraging met zich meebrengt. Als uw reactietijd op waardeverandering van cruciaal belang is, wilt u misschien een korter lopend gemiddelde gebruiken of de samplefrequentie verhogen (vaker meten).
Verder gaan.
initialiseren: Toen ik het had over het initialiseren van accumulator- en vertragingselementen, zei ik dat u ze allemaal op 0 moet initialiseren. Als alternatief kunt u de vertragingslijn initialiseren op alles wat u maar wilt, maar de accumulator zou moeten beginnen als een som van de nieuwste N-elementen in de vertragingslijn (waarbij N is het aantal elementen in uw lopende gemiddelde). Als de accumulator start als een andere waarde, is het berekende gemiddelde verkeerd - ofwel te laag of te hoog, altijd met dezelfde hoeveelheid (uitgaande van dezelfde beginvoorwaarden). Ik stel voor dat je probeert te achterhalen waarom dit zo is door een "pen-en-papiersimulatie" te gebruiken.
accumulatorgrootte: Houd er ook rekening mee dat de accumulator groot genoeg moet zijn om de som van alle elementen in de vertragingslijn op te slaan als ze allemaal positief of negatief zijn. In de praktijk betekent dit dat de accumulator één gegevenstype groter moet zijn dan de vertragingslijnelementen en moet worden ondertekend, als de vertragingslijnelementen zijn ondertekend.
truc: lange vertragingslijnen nemen veel geheugen in beslag. Dat kan al snel een probleem worden. Als je geheugen erg beperkt is en je niet veel om nauwkeurigheid geeft, kun je het lopende gemiddelde benaderen door vertraging volledig weg te laten en in plaats daarvan dit te doen: trek 1/N * accumulator af van accumulator en voeg een nieuwe waarde toe (op voorbeeld van 8 langlopend gemiddelde: accumulator = accumulator * 7/8 + newValue). Deze methode geeft een verkeerd resultaat, maar het is een goede methode om het lopend gemiddelde te berekenen als je weinig geheugen hebt.
taalkunde: "lopend gemiddelde/gemiddelde" wordt meestal gebruikt wanneer wordt verwezen naar real-time gemiddelden, terwijl "bewegend gemiddelde/gemiddelde" meestal betekent dat het algoritme wordt uitgevoerd op statische gegevenssets zoals Excel-spreadsheets.
Stap 6: Conclusie
Ik hoop dat deze instructable gemakkelijk genoeg te begrijpen was en dat het je zal helpen bij je toekomstige projecten. Aarzel niet om vragen te stellen in opmerkingen hieronder als er iets onduidelijk is.
Aanbevolen:
Installatie voor externe Bluetooth GPS-provider voor Android-apparaten: 8 stappen

Installatie voor externe Bluetooth GPS-provider voor Android-apparaten: deze instructable legt uit hoe u uw eigen externe Bluetooth-compatibele GPS voor uw telefoon kunt maken, wat dan ook voor ongeveer $ 10. Materiaallijst: NEO 6M U-blox GPSHC-05 bluetooth-module Kennis van interface Blutooth Low energy-modulesArdui
CP2 Excel gewogen gemiddelde: 14 stappen
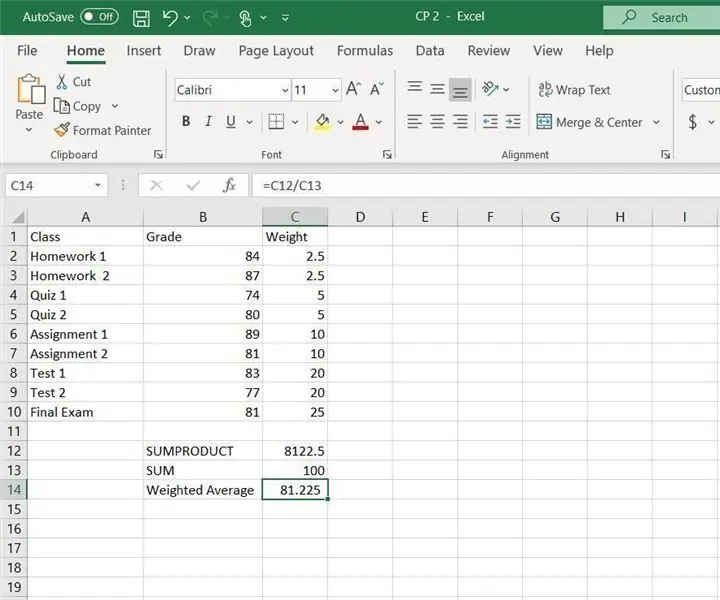
CP2 Excel gewogen gemiddelde: instructies voor het berekenen van het gewogen gemiddelde in Excel. In dit voorbeeld worden de functies SOMPRODUCT en SOM gebruikt in Excel. Het gewogen gemiddelde is handig om het totaalcijfer voor een klas te berekenen
Idee voor doe-het-zelf-activiteit voor weerstations voor 12+ jaar: 4 stappen

Idee voor doe-het-zelf-weerstationactiviteit voor 12-plussers: in deze activiteit zullen deelnemers hun weerstation opzetten, de lucht in sturen en de opnames (licht, temperatuur, vochtigheid) in realtime volgen via de Blynk-app. Bovendien leert u hoe u de geregistreerde waarden publiceert
Bepaal het gemiddelde stroomverbruik van een intermitterend apparaat met laag vermogen: 4 stappen:

Bepaal het gemiddelde stroomverbruik van een intermitterend apparaat met laag stroomverbruik: Inleiding Uit nieuwsgierigheid wilde ik weten hoe lang de batterijen in mijn externe temperatuursensor meegaan. Er zijn twee AA-cellen in serie nodig, maar het is weinig hulp om een ampèremeter in de rij te zetten en naar het display te kijken omdat het stroomverbruik
Helderder dan de gemiddelde beer: 15 stappen

Helderder dan de gemiddelde beer: Ben jij helderder dan de gemiddelde beer? Deze kleine man is dat zeker! Perfect voor gekke wetenschappers, kleine Halloween-scènes of mensen met een verwrongen gevoel voor humor. (Geïnspireerd door deze lamp: http://www.suck.uk.com/product.php?rangeID=104&showBar=1, maar
