
Inhoudsopgave:
- Auteur John Day day@howwhatproduce.com.
- Public 2024-01-30 11:20.
- Laatst gewijzigd 2025-01-23 15:02.
Invoering
Deze gids is bedoeld voor iedereen die geïnteresseerd is in het gebruik van versnellingsmeters en gyroscopen, evenals gecombineerde IMU-apparaten (inertiële meeteenheid) in hun elektronicaprojecten
We behandelen:
- Wat meet een versnellingsmeter?
- Wat meet een gyroscoop (ook bekend als gyro)?
- Hoe analoog-naar-digitaal (ADC) meetwaarden die u van deze sensor krijgt om te zetten in fysieke eenheden (dat zou g zijn voor versnellingsmeter, graden / s voor gyroscoop)
- Hoe u versnellingsmeter- en gyroscoopmetingen combineert om nauwkeurige informatie te verkrijgen over de helling van uw apparaat ten opzichte van het grondvlak
In het hele artikel zal ik proberen de wiskunde tot een minimum te beperken. Als je weet wat sinus/cosinus/tangent is, zou je deze ideeën in je project moeten kunnen begrijpen en gebruiken, ongeacht het platform dat je gebruikt: Arduino, Propeller, Basic Stamp, Atmel-chips, Microchip PIC, enz.
Er zijn mensen die geloven dat je complexe wiskunde nodig hebt om gebruik te maken van een IMU-eenheid (complexe FIR- of IIR-filters zoals Kalman-filters, Parks-McClellan-filters, enz.). Je kunt al die dingen onderzoeken en prachtige maar complexe resultaten behalen. Mijn manier om dingen uit te leggen vereist alleen elementaire wiskunde. Ik ben een groot voorstander van eenvoud. Ik denk dat een systeem dat eenvoudig is, gemakkelijker te besturen en te bewaken is, bovendien hebben veel embedded apparaten niet de kracht en middelen om complexe algoritmen te implementeren die matrixberekeningen vereisen.
Ik zal als voorbeeld een nieuwe IMU-eenheid gebruiken, de Acc_Gyro Accelerometer + Gyro IMU. We gebruiken parameters van dit apparaat in onze onderstaande voorbeelden. Dit apparaat is een goed apparaat om mee te beginnen omdat het uit 2 apparaten bestaat:
- LIS331AL (gegevensblad) - een triaxiale 2G-versnellingsmeter - LPR550AL (gegevensblad) - een 500 graden/sec gyroscoop met twee assen pitch en roll
Samen vertegenwoordigen ze een inertiële meeteenheid van 5 graden van vrijheid. Dat is nog eens een mooie naam! Desalniettemin schuilt achter de mooie naam een zeer handig combinatieapparaat dat we in deze handleiding in detail zullen bespreken en uitleggen.
Stap 1: De versnellingsmeter
Om deze eenheid te begrijpen, beginnen we met de versnellingsmeter. Bij versnellingsmeters is het vaak handig om een doos in de vorm van een kubus voor te stellen met een bal erin. Je kunt je iets anders voorstellen, zoals een koekje of een donut, maar ik stel me een bal voor:
Als we deze doos meenemen naar een plaats zonder zwaartekrachtvelden of zonder andere velden die de positie van de bal kunnen beïnvloeden, zal de bal gewoon in het midden van de doos drijven. Je kunt je voorstellen dat de doos zich in de ruimte bevindt, ver weg van alle kosmische lichamen, of als zo'n plek moeilijk te vinden is, stel je dan op zijn minst een ruimtevaartuig voor dat rond de planeet cirkelt waar alles in gewichtloze staat is. Op de afbeelding hierboven kun je zien dat we aan elke as een paar muren toewijzen (we hebben de muur Y+ verwijderd zodat we in de doos kunnen kijken). Stel je voor dat elke muur drukgevoelig is. Als we de doos plotseling naar links verplaatsen (we versnellen hem met versnelling 1g = 9,8m/s^2), dan raakt de bal de muur X-. We meten vervolgens de drukkracht die de bal op de muur uitoefent en geven een waarde van -1g op de X-as.
Houd er rekening mee dat de versnellingsmeter daadwerkelijk een kracht detecteert die in de tegenovergestelde richting van de versnellingsvector is gericht. Deze kracht wordt vaak traagheidskracht of fictieve kracht genoemd. Een ding dat je hiervan moet leren, is dat een versnellingsmeter de versnelling indirect meet door een kracht die op een van de muren wordt uitgeoefend (volgens ons model kan het een veer zijn of iets anders in echte versnellingsmeters). Deze kracht kan worden veroorzaakt door de versnelling, maar zoals we in het volgende voorbeeld zullen zien, wordt deze niet altijd veroorzaakt door versnelling.
Als we ons model nemen en het op aarde plaatsen, valt de bal op de Z-muur en oefent een kracht van 1g uit op de onderste muur, zoals weergegeven in de onderstaande afbeelding:
In dit geval beweegt de doos niet, maar krijgen we nog steeds een waarde van -1g op de Z-as. De druk die de bal op de muur heeft uitgeoefend, werd veroorzaakt door een zwaartekracht. In theorie zou het een ander soort kracht kunnen zijn - als je je bijvoorbeeld voorstelt dat onze bal van metaal is, kan het plaatsen van een magneet naast de doos de bal verplaatsen zodat deze een andere muur raakt. Dit werd gezegd om te bewijzen dat de versnellingsmeter in wezen kracht meet en niet versnelling. Het gebeurt gewoon dat versnelling een traagheidskracht veroorzaakt die wordt opgevangen door het krachtdetectiemechanisme van de versnellingsmeter.
Hoewel dit model niet precies is hoe een MEMS-sensor is geconstrueerd, is het vaak handig bij het oplossen van problemen met de versnellingsmeter. Er zijn eigenlijk vergelijkbare sensoren met metalen ballen erin, ze worden kantelschakelaars genoemd, maar ze zijn primitiever en meestal kunnen ze alleen zien of het apparaat binnen een bepaald bereik helt of niet, niet de mate van helling.
Tot nu toe hebben we de output van de accelerometer op een enkele as geanalyseerd en dit is alles wat je krijgt met accelerometers met een enkele as. De echte waarde van triaxiale versnellingsmeters komt van het feit dat ze traagheidskrachten op alle drie de assen kunnen detecteren. Laten we teruggaan naar ons doosmodel, en laten we de doos 45 graden naar rechts draaien. De bal zal nu 2 muren raken: Z- en X- zoals weergegeven in de onderstaande afbeelding:
De waarden van 0,71 zijn niet willekeurig, ze zijn eigenlijk een benadering voor SQRT(1/2). Dit zal duidelijker worden naarmate we ons volgende model voor de versnellingsmeter introduceren.
In het vorige model hebben we de zwaartekracht vastgelegd en onze denkbeeldige doos geroteerd. In de laatste 2 voorbeelden hebben we de uitvoer in 2 verschillende boxposities geanalyseerd, terwijl de krachtvector constant bleef. Hoewel dit nuttig was om te begrijpen hoe de versnellingsmeter interageert met krachten van buitenaf, is het praktischer om berekeningen uit te voeren als we het coördinatensysteem op de assen van de versnellingsmeter fixeren en ons voorstellen dat de krachtvector om ons heen draait.
Kijk eens naar het model hierboven, ik heb de kleuren van de assen behouden, zodat je een mentale overgang kunt maken van het vorige model naar het nieuwe. Stelt u zich eens voor dat elke as in het nieuwe model loodrecht staat op de respectieve vlakken van de doos in het vorige model. De vector R is de krachtvector die de versnellingsmeter meet (het kan de zwaartekracht zijn of de traagheidskracht uit de bovenstaande voorbeelden of een combinatie van beide). Rx, Ry, Rz zijn projectie van de R-vector op de X-, Y-, Z-assen. Let op de volgende relatie:
R^2 = Rx^2 + Ry^2 + Rz^2 (Vgl. 1)
wat in feite het equivalent is van de stelling van Pythagoras in 3D.
Onthoud dat ik je een beetje eerder heb verteld dat de waarden van SQRT(1/2) ~ 0,71 niet willekeurig zijn. Als je ze in de bovenstaande formule invult, kunnen we na ons te herinneren dat onze zwaartekracht 1 g was, verifiëren dat:
1^2 = (-SQRT(1/2))^2 + 0 ^2 + (-SQRT(1/2))^2
eenvoudig door R=1, Rx = -SQRT(1/2), Ry = 0, Rz = -SQRT(1/2) in Vgl.1 te vervangen
Na een lange inleiding van theorie komen we dichter bij echte versnellingsmeters. De waarden Rx, Ry, Rz zijn eigenlijk lineair gerelateerd aan de waarden die uw real-life accelerometer zal uitvoeren en die u kunt gebruiken voor het uitvoeren van verschillende berekeningen.
Voordat we daar aankomen, laten we het hebben over de manier waarop versnellingsmeters deze informatie aan ons zullen leveren. De meeste versnellingsmeters vallen in twee categorieën: digitaal en analoog. Digitale versnellingsmeters geven u informatie met behulp van een serieel protocol zoals I2C, SPI of USART, terwijl analoge versnellingsmeters een spanningsniveau uitvoeren binnen een vooraf gedefinieerd bereik dat u moet converteren naar een digitale waarde met behulp van een ADC-module (analoog naar digitaal converter). Ik zal niet in detail treden over hoe ADC werkt, deels omdat het zo'n uitgebreid onderwerp is en deels omdat het per platform verschilt. Sommige microcontrollers hebben ingebouwde ADC-modules, sommige hebben externe componenten nodig om de ADC-conversies uit te voeren. Het maakt niet uit welk type ADC-module u gebruikt, u krijgt een waarde in een bepaald bereik. Een 10-bit ADC-module zal bijvoorbeeld een waarde in het bereik van 0..1023 uitvoeren, merk op dat 1023 = 2^10 -1. Een 12-bits ADC-module geeft een waarde uit in het bereik van 0..4095, let op: 4095 = 2^12-1.
Laten we verder gaan met een eenvoudig voorbeeld, stel dat onze 10bit ADC-module ons de volgende waarden gaf voor de drie versnellingsmeterkanalen (assen):
AdcRx = 586 AdcRy = 630 AdcRz = 561
Elke ADC-module heeft een referentiespanning, laten we aannemen dat dit in ons voorbeeld 3,3V is. Om een 10-bits adc-waarde om te zetten in spanning gebruiken we de volgende formule:
VoltsRx = AdcRx * Vref / 1023
Een korte opmerking hier: dat voor 8-bits ADC de laatste deler 255 = 2 ^ 8 -1 zou zijn, en voor 12-bits ADC zou de laatste deler 4095 = 2 ^ 12 -1 zijn.
Als we deze formule toepassen op alle 3 de kanalen, krijgen we:
VoltsRx = 586 * 3.3V / 1023 =~ 1.89V (we ronden alle resultaten af op 2 decimalen) VoltsRy = 630 * 3.3V / 1023 =~ 2.03V VoltsRz = 561 * 3.3V / 1023 =~ 1.81V
Elke versnellingsmeter heeft een nul-g spanningsniveau, je kunt het vinden in de specificaties, dit is de spanning die overeenkomt met 0g. Om een ondertekende spanningswaarde te krijgen, moeten we de verschuiving vanaf dit niveau berekenen. Laten we zeggen dat ons 0g-spanningsniveau VzeroG = 1,65V is. We berekenen de spanningsverschuivingen van nul-g spanning als volgt:
DeltaVoltsRx = 1,89V - 1,65V = 0,24V DeltaVoltsRy = 2,03V - 1,65V = 0,38V DeltaVoltsRz = 1,81V - 1,65V = 0,16V
We hebben nu onze versnellingsmeterwaarden in Volt, het is nog steeds niet in g (9,8 m/s^2), om de uiteindelijke conversie uit te voeren passen we de gevoeligheid van de versnellingsmeter toe, meestal uitgedrukt in mV/g. Laten we zeggen onze Gevoeligheid = 478.5mV/g = 0.4785V/g. Gevoeligheidswaarden zijn te vinden in de specificaties van de accelerometer. Om de uiteindelijke krachtwaarden uitgedrukt in g te krijgen, gebruiken we de volgende formule:
Rx = DeltaVoltsRx / Gevoeligheid
Rx = 0,24V / 0,4785V/g =~ 0,5g Ry = 0,38V / 0,4785V/g =~ 0,79g Rz = 0,16V / 0,4785V/g =~ 0,33g
We zouden natuurlijk alle stappen in één formule kunnen combineren, maar ik heb alle stappen doorlopen om duidelijk te maken hoe je van ADC-uitlezingen naar een krachtvectorcomponent uitgedrukt in g gaat.
Rx = (AdcRx * Vref / 1023 - VzeroG) / Gevoeligheid (Eq.2) Ry = (AdcRy * Vref / 1023 - VzeroG) / Gevoeligheid Rz = (AdcRz * Vref / 1023 - VzeroG) / Gevoeligheid
We hebben nu alle 3 componenten die onze traagheidskrachtvector definiëren. Als het apparaat niet onderhevig is aan andere krachten dan zwaartekracht, kunnen we aannemen dat dit de richting is van onze zwaartekrachtvector. Als u de helling van het apparaat ten opzichte van de grond wilt berekenen, kunt u de hoek tussen deze vector en de Z-as berekenen. Als u ook geïnteresseerd bent in de hellingsrichting per as, kunt u dit resultaat opsplitsen in 2 componenten: helling op de X- en Y-as die kan worden berekend als de hoek tussen gravitatievector en X / Y-assen. Het berekenen van deze hoeken is eenvoudiger dan je zou denken, nu we de waarden voor Rx, Ry en Rz hebben berekend. Laten we teruggaan naar ons laatste accelerometermodel en wat aanvullende notaties maken:
De hoeken waarin we geïnteresseerd zijn, zijn de hoeken tussen de X-, Y-, Z-assen en de krachtvector R. We zullen deze hoeken definiëren als Axr, Ayr, Azr. Je kunt aan de rechthoekige driehoek, gevormd door R en Rx, zien dat:
cos(Axr) = Rx / R, en op dezelfde manier: cos(Ayr) = Ry / R cos(Azr) = Rz / R
Uit vergelijking 1 kunnen we afleiden dat R = SQRT(Rx^2 + Ry^2 + Rz^2).
We kunnen nu onze hoeken vinden door de functie arccos() te gebruiken (de inverse functie cos()):
Axr = arccos(Rx/R) Ayr = arccos(Ry/R) Azr = arccos(Rz/R)
We hebben een lange weg afgelegd om het accelerometermodel uit te leggen, om tot deze formules te komen. Afhankelijk van uw toepassingen wilt u misschien tussenliggende formules gebruiken die we hebben afgeleid. We zullen binnenkort ook het gyroscoopmodel introduceren, en we zullen zien hoe versnellingsmeter- en gyroscoopgegevens kunnen worden gecombineerd om nog nauwkeurigere schattingen van de helling te geven.
Maar laten we, voordat we dat doen, nog wat handigere notaties doen:
cosX = cos(Axr) = Rx / R cosy = cos(Ayr) = Ry / R cosZ = cos(Azr) = Rz / R
Dit triplet wordt vaak Direction Cosinus genoemd en vertegenwoordigt in feite de eenheidsvector (vector met lengte 1) die dezelfde richting heeft als onze R-vector. U kunt eenvoudig verifiëren dat:
SQRT(cosX^2 + cosY^2 + cosZ^2) = 1
Dit is een mooie eigenschap omdat het ons ontslaat van het bewaken van de modulus (lengte) van de R-vector. Vaak als we alleen geïnteresseerd zijn in de richting van onze traagheidsvector, is het logisch om de modulus te normaliseren om andere berekeningen te vereenvoudigen.
Stap 2: Gyroscoop
We gaan geen gelijkwaardig boxmodel voor de gyroscoop introduceren zoals we deden voor accelerometer, in plaats daarvan gaan we direct naar het tweede accelerometermodel en laten we zien wat de gyroscoop meet volgens dit model.
Elk gyroscoopkanaal meet de rotatie rond een van de assen. Een 2-assige gyroscoop meet bijvoorbeeld de rotatie rond (of sommigen zeggen "ongeveer") de X- en Y-assen. Laten we enkele notaties maken om deze rotatie in getallen uit te drukken. Laten we eerst definiëren:
Rxz - is de projectie van de traagheidskrachtvector R op het XZ-vlak Ryz - is de projectie van de traagheidskrachtvector R op het YZ-vlak
Uit de rechthoekige driehoek gevormd door Rxz en Rz, met behulp van de stelling van Pythagoras krijgen we:
Rxz^2 = Rx^2 + Rz^2, en op dezelfde manier: Ryz^2 = Ry^2 + Rz^2
merk ook op dat:
R^2 = Rxz^2 + Ry^2, dit kan worden afgeleid uit vergelijkingen van Eq.1 en hoger, of het kan worden afgeleid van een rechthoekige driehoek gevormd door R en Ryz R^2 = Ryz^2 + Rx^2
We gaan deze formules in dit artikel niet gebruiken, maar het is handig om de relatie tussen alle waarden in ons model te noteren.
In plaats daarvan gaan we de hoek tussen de Z-as en Rxz, Ryz-vectoren als volgt definiëren:
Axz - is de hoek tussen de Rxz (projectie van R op het XZ-vlak) en de Z-as Ayz - is de hoek tussen de Ryz (projectie van R op het YZ-vlak) en de Z-as
Nu komen we dichter bij wat de gyroscoop meet. Gyroscoop meet de snelheid van veranderingen van de hierboven gedefinieerde hoeken. Met andere woorden, het geeft een waarde af die lineair gerelateerd is aan de veranderingssnelheid van deze hoeken. Laten we, om dit te verklaren, aannemen dat we de rotatiehoek rond as Y hebben gemeten (dat zou Axz-hoek zijn) op tijdstip t0, en we definiëren het als Axz0, vervolgens hebben we deze hoek op een later tijdstip t1 gemeten en het was Axz1. Het wijzigingspercentage wordt als volgt berekend:
TariefAxz = (Axz1 - Axz0) / (t1 - t0).
Als we Axz uitdrukken in graden en tijd in seconden, dan wordt deze waarde uitgedrukt in graden/s. Dit is wat een gyroscoop meet.
In de praktijk geeft een gyroscoop (tenzij het een speciale digitale gyroscoop is) zelden een waarde uitgedrukt in graden/s. Hetzelfde als voor de accelerometer, je krijgt een ADC-waarde die je moet converteren naar deg/s met een formule die vergelijkbaar is met Eq. 2 die we hebben gedefinieerd voor versnellingsmeter. Laten we de ADC naar deg/s-conversieformule voor gyroscoop introduceren (we nemen aan dat we een 10bit ADC-module gebruiken, voor 8bit ADC vervang je 1023 door 255, voor 12bit ADC vervang je 1023 door 4095).
RateAxz = (AdcGyroXZ * Vref / 1023 - VzeroRate) / Gevoeligheid Eq.3 RateAyz = (AdcGyroYZ * Vref / 1023 - VzeroRate) / Gevoeligheid
AdcGyroXZ, AdcGyroYZ - worden verkregen uit onze adc-module en ze vertegenwoordigen de kanalen die de rotatie van de projectie van de R-vector in XZ respectievelijk in YZ-vlakken meten, wat overeenkomt met het zeggen dat de rotatie respectievelijk rond de Y- en X-assen is gedaan.
Vref - is de ADC-referentiespanning die we in het onderstaande voorbeeld 3,3 V zullen gebruiken VzeroRate - is de nultariefspanning, met andere woorden de spanning die de gyroscoop uitvoert wanneer deze niet wordt gedraaid, voor het Acc_Gyro-bord is dit bijvoorbeeld 1.23V (u kunt deze waarden vinden in de specificaties) Gevoeligheid - is de gevoeligheid van uw gyroscoop het wordt uitgedrukt in mV / (deg / s) vaak geschreven als mV/deg/s, het vertelt u in feite hoeveel mV zal de output van de gyroscoop neemt toe als u de rotatiesnelheid met één deg/s verhoogt. De gevoeligheid van Acc_Gyro board is bijvoorbeeld 2mV/deg/s of 0.002V/deg/s
Laten we een voorbeeld nemen, stel dat onze ADC-module de volgende waarden heeft geretourneerd:
AdcGyroXZ = 571 AdcGyroXZ = 323
Met behulp van de bovenstaande formule en met behulp van de specs-parameters van het Acc_Gyro-bord krijgen we:
RateAxz = (571 * 3.3V / 1023 - 1.23V) / (0.002V/deg/s) =~ 306 deg/s RateAyz = (323 * 3.3V / 1023 - 1.23V) / (0.002V/deg/s) =~ -94 graden/s
Met andere woorden, het apparaat roteert rond de Y-as (of we kunnen zeggen dat het roteert in het XZ-vlak) met een snelheid van 306 graden/s en rond de X-as (of we kunnen zeggen dat het roteert in het YZ-vlak) met een snelheid van - 94 graden/sec. Houd er rekening mee dat het minteken betekent dat het apparaat in de tegenovergestelde richting draait van de conventionele positieve richting. Volgens afspraak is één draairichting positief. Een goed specificatieblad van de gyroscoop zal je laten zien welke richting positief is, anders moet je het vinden door met het apparaat te experimenteren en op te merken in welke draairichting de spanning op de uitgangspen toeneemt. Dit kunt u het beste doen met een oscilloscoop, aangezien zodra u de rotatie stopt, de spanning terugvalt naar het nultarief. Als u een multimeter gebruikt, moet u gedurende ten minste enkele seconden een constante rotatiesnelheid aanhouden en de spanning tijdens deze rotatie noteren en deze vervolgens vergelijken met de nultariefspanning. Als deze groter is dan de nultariefspanning, betekent dit dat de draairichting positief is.
Stap 3: De versnellingsmeter en gyro combineren
Alles bij elkaar - Accelerometer- en gyroscoopgegevens combineren
Als u dit artikel leest, heeft u waarschijnlijk een IMU-apparaat aangeschaft of bent u van plan er een aan te schaffen, of bent u van plan er een te bouwen met afzonderlijke versnellingsmeter- en gyroscoopapparaten.
De eerste stap bij het gebruik van een gecombineerd IMU-apparaat dat een versnellingsmeter en een gyroscoop combineert, is het uitlijnen van hun coördinatensystemen. De eenvoudigste manier om dit te doen, is door het coördinatensysteem van de versnellingsmeter te kiezen als uw referentiecoördinatensysteem. De meeste gegevensbladen van versnellingsmeters geven de richting van de X-, Y-, Z-assen weer ten opzichte van het beeld van de fysieke chip of het apparaat. Hier zijn bijvoorbeeld de richtingen van de X-, Y-, Z-assen zoals weergegeven in de specificaties voor het Acc_Gyro-bord:
Volgende stappen zijn:
Identificeer de gyroscoopuitgangen die overeenkomen met RateAxz, RateAyz-waarden die hierboven zijn besproken. Bepaal of deze uitgangen moeten worden omgekeerd vanwege de fysieke positie van de gyroscoop ten opzichte van de versnellingsmeter
Ga er niet vanuit dat als een gyroscoop een uitgang heeft die is gemarkeerd met X of Y, deze overeenkomt met elke as in het coördinatensysteem van de versnellingsmeter, zelfs als deze uitgang deel uitmaakt van een IMU-eenheid. De beste manier is om het te testen. Ervan uitgaande dat u de positie van de gyroscoop ten opzichte van de versnellingsmeter hebt vastgesteld. Er wordt aangenomen dat de randen van de gyro en de versnellingsmeter evenwijdig aan elkaar zijn, d.w.z. dat je de gyro onder een veelvoud van 90 graden plaatst ten opzichte van de chip van de versnellingsmeter. Als je een IMU-bord hebt gekocht, is de kans groot dat ze al op deze manier zijn uitgelijnd. We gaan in dit artikel geen modellen bespreken waarbij de gyroscoop in een onregelmatige hoek is geplaatst ten opzichte van de accelerometer (laten we zeggen 45 of 30 graden), hoewel dit in sommige toepassingen nuttig kan zijn.
Hier is een voorbeeldreeks om te bepalen welke uitvoer van de gyroscoop overeenkomt met de hierboven besproken RateAxz-waarde.
- begin met het plaatsen van het apparaat in horizontale positie. Zowel de X- als de Y-uitgangen van de accelerometer zouden de nul-g-spanning uitvoeren (bijvoorbeeld voor Acc_Gyro-bord is dit 1,65V)
- begin vervolgens het apparaat rond de Y-as te draaien, een andere manier om het te zeggen is dat je het apparaat in het XZ-vlak draait, zodat de uitgangen van de X- en Z-versnellingsmeter veranderen en de Y-uitgang constant blijft. - terwijl het apparaat met een constante snelheid wordt gedraaid, noteer welke gyroscoopuitgang verandert, de andere gyroscoopuitgangen moeten constant blijven - de gyroscoopuitgang die veranderde tijdens de rotatie rond de Y-as (rotatie in XZ-vlak) zal de ingangswaarde leveren voor AdcGyroXZ, van waaruit we berekenen RateAxz - de laatste stap is om ervoor te zorgen dat de draairichting overeenkomt met ons model, in sommige gevallen moet u de RateAxz-waarde mogelijk omkeren vanwege de fysieke positie van de gyroscoop ten opzichte van de versnellingsmeter - voer de bovenstaande test opnieuw uit en draai het apparaat rond de Y-as, controleer deze keer de X-uitgang van de accelerometer (AdcRx in ons model). Als AdcRx groeit (de eerste 90 graden rotatie vanuit horizontale positie), dan zou AdcGyroXZ ook moeten groeien. Anders moet u RateAxz omkeren, u kunt dit bereiken door een tekenfactor in Vgl.3 als volgt in te voeren:
RateAxz = InvertAxz * (AdcGyroXZ * Vref / 1023 - VzeroRate) / Gevoeligheid, waarbij InvertAxz 1 of -1 is
dezelfde test kan worden gedaan voor RateAyz, door het apparaat rond de X-as te draaien, en u kunt bepalen welke gyroscoopuitgang overeenkomt met RateAyz en of deze moet worden omgekeerd. Zodra u de waarde voor InvertAyz hebt, moet u de volgende formule gebruiken om RateAyz te berekenen:
RateAyz = InvertAyz * (AdcGyroYZ * Vref / 1023 - VzeroRate) / Gevoeligheid
Als je deze tests op het Acc_Gyro-bord zou doen, zou je de volgende resultaten krijgen:
- de uitgangspen voor RateAxz is GX4 en InvertAxz = -1. - de uitgangspen voor RateAyz is GY4 en InvertAyz = -1
Vanaf dit punt gaan we ervan uit dat u uw IMU zo hebt ingesteld dat u de juiste waarden kunt berekenen voor Axr, Ayr, Azr (zoals gedefinieerd in Deel 1. Accelerometer) en RateAxz, RateAyz (zoals gedefinieerd in Deel 2. Gyroscoop). Vervolgens analyseren we de relaties tussen deze waarden die nuttig blijken te zijn voor het verkrijgen van een nauwkeurigere schatting van de helling van het apparaat ten opzichte van het grondvlak.
Je vraagt je misschien af op dit punt, als het accelerometermodel ons al hellingshoeken van Axr, Ayr, Azr gaf, waarom zouden we ons dan druk maken over de gyroscoopgegevens? Het antwoord is simpel: gegevens van de versnellingsmeter zijn niet altijd 100% te vertrouwen. Er zijn verschillende redenen, onthoud dat de versnellingsmeter traagheidskracht meet, een dergelijke kracht kan worden veroorzaakt door zwaartekracht (en idealiter alleen door zwaartekracht), maar het kan ook worden veroorzaakt door versnelling (beweging) van het apparaat. Als gevolg hiervan is de versnellingsmeter, zelfs als deze zich in een relatief stabiele toestand bevindt, nog steeds erg gevoelig voor trillingen en mechanische ruis in het algemeen. Dit is de belangrijkste reden waarom de meeste IMU-systemen een gyroscoop gebruiken om eventuele accelerometerfouten glad te strijken. Maar hoe wordt dit gedaan? En is de gyroscoop vrij van ruis?
De gyroscoop is niet vrij van ruis, maar omdat hij rotatie meet, is hij minder gevoelig voor lineaire mechanische bewegingen, het soort ruis waar de accelerometer last van heeft, maar gyroscopen hebben andere soorten problemen, zoals bijvoorbeeld drift (niet terugkeren naar nul-rate waarde wanneer de rotatie stopt). Desalniettemin kunnen we door middel van gegevens die afkomstig zijn van versnellingsmeter en gyroscoop een relatief betere schatting krijgen van de huidige apparaathelling dan we zouden verkrijgen door alleen de versnellingsmetergegevens te gebruiken.
In de volgende stappen zal ik een algoritme introduceren dat is geïnspireerd op enkele ideeën die in het Kalman-filter worden gebruikt, maar het is veel eenvoudiger en gemakkelijker te implementeren op embedded apparaten. Laten we eerst eens kijken wat we willen dat ons algoritme berekent. Welnu, het is de richting van de zwaartekrachtvector R = [Rx, Ry, Rz] waaruit we andere waarden kunnen afleiden, zoals Axr, Ayr, Azr of cosX, cosY, cosZ die ons een idee zullen geven over de helling van ons apparaat ten opzichte van het grondvlak bespreken we de relatie tussen deze waarden in Deel 1. Je zou kunnen zeggen - hebben we deze waarden Rx, Ry, Rz niet al uit Vgl.2 in Deel 1 ? Nou ja, maar onthoud dat deze waarden alleen zijn afgeleid van versnellingsmetergegevens, dus als u ze rechtstreeks in uw toepassing zou gebruiken, zou u meer ruis kunnen krijgen dan uw toepassing kan verdragen. Laten we, om verdere verwarring te voorkomen, de metingen van de versnellingsmeter als volgt herdefiniëren:
Racc - is de traagheidskrachtvector zoals gemeten door een versnellingsmeter, die uit de volgende componenten bestaat (projecties op X-, Y-, Z-assen):
RxAcc = (AdcRx * Vref / 1023 - VzeroG) / Gevoeligheid RyAcc = (AdcRy * Vref / 1023 - VzeroG) / Gevoeligheid RzAcc = (AdcRz * Vref / 1023 - VzeroG) / Gevoeligheid
Tot nu toe hebben we een set meetwaarden die we puur uit accelerometer ADC-waarden kunnen halen. We noemen deze verzameling gegevens een 'vector' en gebruiken de volgende notatie.
Racc = [RxAcc, RyAcc, RzAcc]
Omdat deze componenten van Racc kunnen worden verkregen uit versnellingsmetergegevens, kunnen we het beschouwen als een invoer voor ons algoritme.
Houd er rekening mee dat, omdat Racc de zwaartekracht meet, je gelijk hebt als je aanneemt dat de lengte van deze vector gedefinieerd als volgt gelijk is aan of dichtbij 1 g ligt.
|Racc| = SQRT(RxAcc^2 +RyAcc^2 + RzAcc^2), Om zeker te zijn is het echter zinvol om deze vector als volgt bij te werken:
Racc(genormaliseerd) = [RxAcc/|Racc|, RyAcc/|Racc|, RzAcc/|Racc|].
Dit zorgt ervoor dat de lengte van uw genormaliseerde Racc-vector altijd 1 is.
Vervolgens introduceren we een nieuwe vector en noemen we deze
Rust = [RxEst, RyEst, RzEst]
Dit is de uitvoer van ons algoritme, dit zijn gecorrigeerde waarden op basis van gyroscoopgegevens en op basis van geschatte gegevens uit het verleden.
Dit is wat ons algoritme zal doen: - versnellingsmeter vertelt ons: "Je bent nu op positie Racc" - we zeggen "Dank je, maar laat me het controleren", - corrigeer deze informatie vervolgens met gyroscoopgegevens en met eerdere rustgegevens en we geven een nieuwe geschatte vector Rest. - we beschouwen Rust als onze "beste gok" met betrekking tot de huidige positie van het apparaat.
Laten we kijken hoe we het kunnen laten werken.
We beginnen onze reeks door onze versnellingsmeter te vertrouwen en toe te wijzen:
Rust(0) = Racc(0)
Onthoud trouwens dat Rest en Racc vectoren zijn, dus de bovenstaande vergelijking is slechts een eenvoudige manier om 3 sets vergelijkingen te schrijven en herhaling te voorkomen:
RxEst(0) = RxAcc(0) RyEst(0) = RyAcc(0) RzEst(0) = RzAcc(0)
Vervolgens zullen we regelmatige metingen doen met gelijke tijdsintervallen van T seconden, en we zullen nieuwe metingen verkrijgen die we zullen definiëren als Racc(1), Racc(2), Racc(3) enzovoort. We geven ook nieuwe schattingen met elke tijdsinterval Rust(1), Rust(2), Rust(3) enzovoort.
Stel dat we bij stap n zijn. We hebben twee bekende sets met waarden die we willen gebruiken:
Rest(n-1) - onze vorige schatting, met Rest(0) = Racc(0) Racc(n) - onze huidige versnellingsmetermeting
Voordat we Rest(n) kunnen berekenen, introduceren we een nieuwe meetwaarde, die we kunnen verkrijgen uit onze gyroscoop en een eerdere schatting.
We noemen het Rgyro, en het is ook een vector die uit 3 componenten bestaat:
Rgyro = [RxGyro, RyGyro, RzGyro]
We zullen deze vector component voor component berekenen. We beginnen met RxGyro.
Laten we beginnen met het observeren van de volgende relatie in ons gyroscoopmodel, uit de rechthoekige driehoek gevormd door Rz en Rxz kunnen we dat afleiden:
tan(Axz) = Rx/Rz => Axz = atan2(Rx, Rz)
Atan2 is misschien een functie die u nog nooit eerder hebt gebruikt, het is vergelijkbaar met atan, behalve dat het waarden retourneert in het bereik van (-PI, PI) in tegenstelling tot (-PI/2, PI/2) zoals geretourneerd door atan, en het duurt 2 argumenten in plaats van één. Het stelt ons in staat om de twee waarden van Rx, Rz om te zetten in hoeken in het volledige bereik van 360 graden (-PI tot PI). U kunt hier meer lezen over atan2.
Dus als we RxEst(n-1), en RzEst(n-1) kennen, kunnen we vinden:
Axz(n-1) = atan2(RxEst(n-1), RzEst(n-1)).
Onthoud dat de gyroscoop de veranderingssnelheid van de Axz-hoek meet. We kunnen de nieuwe hoek Axz(n) dus als volgt schatten:
Axz(n) = Axz(n-1) + RateAxz(n) * T
Onthoud dat RateAxz kan worden verkregen uit onze gyroscoop ADC-metingen. Een preciezere formule kan een gemiddelde rotatiesnelheid gebruiken die als volgt wordt berekend:
RateAxzAvg = (RateAxz(n) + RateAxz(n-1)) / 2 Axz(n) = Axz(n-1) + RateAxzAvg * T
Op dezelfde manier kunnen we vinden:
Ayz(n) = Ayz(n-1) + RateAyz(n) * T
Ok dus nu hebben we Axz(n) en Ayz(n). Waar gaan we vanaf hier om RxGyro/RyGyro af te trekken? Van verg. 1 kunnen we de lengte van vector Rgyro als volgt schrijven:
|Rgyro| = SQRT(RxGyro^2 + RyGyro^2 + RzGyro^2)
Ook omdat we onze Racc-vector hebben genormaliseerd, mogen we aannemen dat de lengte 1 is en niet is veranderd na de rotatie, dus het is relatief veilig om te schrijven:
|Rgyro| = 1
Laten we een tijdelijke kortere notatie gebruiken voor de onderstaande berekeningen:
x =RxGyro, y=RyGyro, z=RzGyro
Met behulp van de bovenstaande relaties kunnen we schrijven:
x = x / 1 = x / SQRT(x^2+y^2+z^2)
Laten we de teller en noemer van een breuk delen door SQRT(x^2 + z^2)
x = (x / SQRT(x^2 + z^2)) / SQRT((x^2 + y^2 + z^2) / (x^2 + z^2))
Merk op dat x / SQRT(x^2 + z^2) = sin(Axz), dus:
x = sin(Axz) / SQRT (1 + y^2 / (x^2 + z^2))
Vermenigvuldig nu de teller en noemer van de breuk binnen SQRT met z^2
x = sin(Axz) / SQRT (1 + y^2 * z ^2 / (z^2 * (x^2 + z^2)))
Merk op dat z / SQRT(x^2 + z^2) = cos(Axz) en y / z = tan(Ayz), dus uiteindelijk:
x = sin(Axz) / SQRT (1 + cos(Axz)^2 * tan(Ayz)^2)
Terugkerend naar onze notatie krijgen we:
RxGyro = sin(Axz(n)) / SQRT (1 + cos(Axz(n))^2 * tan(Ayz(n))^2)
op dezelfde manier vinden we dat
RyGyro = sin(Ayz(n)) / SQRT (1 + cos(Ayz(n))^2 * tan(Axz(n))^2)
Nu kunnen we eindelijk vinden:
RzGyro = Teken(RzGyro)*SQRT(1 - RxGyro^2 - RyGyro^2).
Waarbij Sign(RzGyro) = 1 wanneer RzGyro>=0, en Sign(RzGyro) = -1 wanneer RzGyro<0.
Een eenvoudige manier om dit te schatten is door te nemen:
Teken(RzGyro) = Teken(RzEst(n-1))
Wees in de praktijk voorzichtig wanneer RzEst(n-1) dicht bij 0 ligt. U kunt in dit geval de gyrofase helemaal overslaan en toewijzen: Rgyro = Rest(n-1). Rz wordt gebruikt als referentie voor het berekenen van Axz- en Ayz-hoeken en wanneer deze bijna 0 is, kunnen waarden overlopen en slechte resultaten veroorzaken. U bevindt zich in het domein van grote getallen met drijvende komma waar de implementaties van tan() / atan()-functies mogelijk niet nauwkeurig zijn.
Dus laten we samenvatten wat we tot nu toe hebben, we zijn bij stap n van ons algoritme en we hebben de volgende waarden berekend:
Racc - huidige metingen van onze accelerometer Rgyro - verkregen uit Rest(n-1) en huidige gyroscoopmetingen
Welke waarden gebruiken we om de bijgewerkte schatting Rest(n) te berekenen? Je raadt waarschijnlijk al dat we beide zullen gebruiken. We gebruiken een gewogen gemiddelde, zodat:
Rust(n) = (Racc * w1 + Rgyro * w2) / (w1 + w2)
We kunnen deze formule vereenvoudigen door zowel de teller als de noemer van de breuk te delen door w1.
Rust(n) = (Racc * w1/w1 + Rgyro * w2/w1) / (w1/w1 + w2/w1)
en na vervanging van w2/w1 = wGyro krijgen we:
Rust(n) = (Racc + Rgyro * wGyro) / (1 + wGyro)
In het bovenstaande forum vertelt wGyro ons hoeveel we onze gyro vertrouwen in vergelijking met onze versnellingsmeter. Deze waarde kan experimenteel worden gekozen, meestal zullen waarden tussen 5..20 goede resultaten opleveren.
Het belangrijkste verschil tussen dit algoritme en het Kalman-filter is dat dit gewicht relatief vast is, terwijl in het Kalman-filter de gewichten permanent worden bijgewerkt op basis van de gemeten ruis van de versnellingsmeterwaarden. Het Kalman-filter is erop gericht u "de beste" theoretische resultaten te geven, terwijl dit algoritme u resultaten kan geven die "goed genoeg" zijn voor uw praktische toepassing. U kunt een algoritme implementeren dat wGyro aanpast afhankelijk van bepaalde ruisfactoren die u meet, maar vaste waarden zullen voor de meeste toepassingen goed werken.
We zijn nog maar één stap verwijderd van het verkrijgen van onze bijgewerkte geschatte waarden:
RxEst(n) = (RxAcc + RxGyro * wGyro) / (1 + wGyro) RyEst(n) = (RyAcc + RyGyro * wGyro) / (1 + wGyro) RzEst(n) = (RzAcc + RzGyro * wGyro) / (1 + wGyro)
Laten we nu deze vector opnieuw normaliseren:
R = SQRT(RxEst(n) ^2 + RyEst(n)^2 + RzEst(n)^2)
RxEst(n) = RxEst(n)/R RyEst(n) = RyEst(n)/R RzEst(n) = RzEst(n)/R
En we zijn klaar om onze lus opnieuw te herhalen.
Deze gids verscheen oorspronkelijk op starlino.com, ik heb een paar kleine wijzigingen aangebracht en met toestemming opnieuw geplaatst. Bedankt Starlino!
Aanbevolen:
Squeal & schrapen: 5 stappen
Squeal & Scrape: Dit project kan worden gemaakt door een PCB te frezen met behulp van bestanden op github of door vero-board te gebruiken zoals in de afbeelding. Er is wat soldeerwerk vereist, dus de gebruikelijke apparatuur is nodig: soldeerboutstandaardsoldeerdraadtipreinigerdraadknipperdraadstripperhelpt
Temperatuur CubeSat Ben & Kaiti & Q Hour 1: 8 stappen

Temperature CubeSat Ben & Kaiti & Q Uur 1: Heb je ooit zelf iets willen maken dat naar de ruimte kan worden gestuurd en de temperatuur van een andere planeet kan opnemen? In onze natuurkundeles op de middelbare school kregen we de opdracht om een CubeSat te bouwen met een functionerende arduino met de hoofdvraag Hoe kunnen we
Accelerometer jas: 5 stappen
Accelerometer Jacket: Ontworpen door ThunderLily voor een samenwerking met ontwerper Minika Ko voor de KOllision catwalkshow, het acceleratiejack combineert mode, technologie en kunst. Met behulp van een versnellingsmeter om de bewegingsrichting te detecteren, een microprocessor van de flora en
Een Cubesat bouwen met een Arduino en accelerometer: 5 stappen

Hoe maak je een Cubesat bouwen met een Arduino en Accelerometer .: Onze namen zijn Brock, Eddie en Drew. Het belangrijkste doel van onze natuurkundeles is om van de aarde naar Mars te reizen terwijl we de baan rond Mars simuleren met behulp van een Cube Sat en het verzamelen van gegevens. Het doel van onze groep voor dit project is om gegevens te verzamelen met behulp van een accele
Nog een Arduino-weerstation (ESP-01 & BMP280 & DHT11 & OneWire): 4 stappen
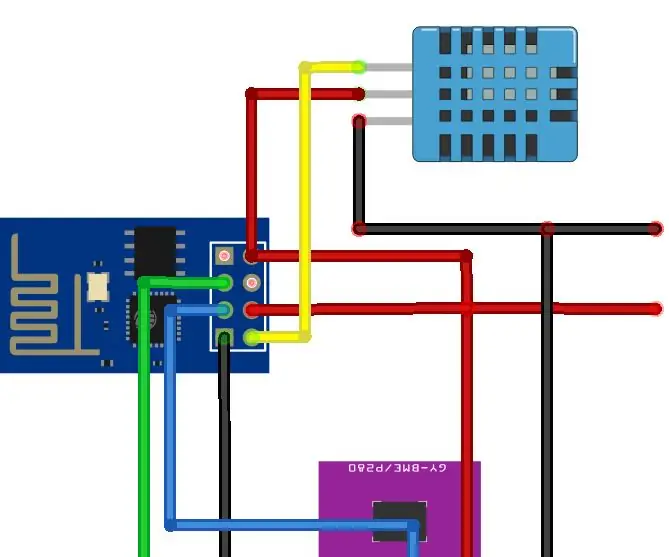
Nog een Arduino-weerstation (ESP-01 & BMP280 & DHT11 & OneWire): hier vindt u een iteratie van het gebruik van OneWire met de weinige pinnen van een ESP-01. Het apparaat dat in deze instructable is gemaakt, maakt verbinding met het wifi-netwerk van uw keuze (u moet de inloggegevens hebben…) Verzamelt sensorische gegevens van een BMP280 en een DHT11
