Som van producten Circuit met behulp van logische poorten - Ajarnpa

2025 Auteur: John Day | [email protected]. Laatst gewijzigd: 2025-01-13 06:57

In deze instructable laat ik je zien hoe je je eigen systeem kunt maken met behulp van de som van producten, een klein beetje Booleaanse algebra en enkele logische poorten. U hoeft niet exact hetzelfde systeem te maken als in deze tutorial, maar u kunt het als richtlijn gebruiken om uw eigen waarheidstabel voor uw circuit te maken.

Stap 1: Maak een waarheidstabel

Zoals ik al eerder zei, hoeft jouw waarheidstabel geen exacte kopie van de mijne te zijn. Je kunt ervoor kiezen om elk type waarheidstabel te maken, of dat nu twee ingangen, drie ingangen of zelfs vier ingangen zijn waar je elk van je scenario's waar kunt maken. Gebruik de bovenstaande tabel als voorbeeld van een waarheidstabel. Ik heb die waarheidstabel gemaakt waar er slechts 2 scenario's zijn waarin de uitvoer waar is.

Stap 2: Leid uw vergelijking af en vereenvoudig deze

Als je eenmaal je waarheidstabel hebt, kun je er een algemene vergelijking voor afleiden. Dit is waar de Booleaanse algebra in het spel komt. Als je eenmaal de algemene vergelijking van je waarheidstabel hebt, kun je verschillende Booleaanse algebra-regels gebruiken (sommige zijn hierboven vermeld) om de vergelijking te vereenvoudigen die tot een eenvoudiger circuit leidt.

Mijn vereenvoudigde vergelijking bleek te zijn:

AB(C + D) + ACD

Stap 3: Verzamel materialen

Als je eenmaal je vereenvoudigde vergelijking hebt, kun je nu materialen verzamelen om je circuit te maken. Dit varieert afhankelijk van uw vergelijking, dus het is misschien niet exact dezelfde lijst als de mijne, maar we zullen dezelfde invoer- en uitvoercomponenten hebben.

Met mijn vergelijking als: AB(C + D) + ACD

Ik zou nodig hebben:

1x drievoudige ingang EN poort

1x OF-poort

1x 4 Ingangen Dip-schakelaar

1x 330 ohm weerstand

1x led

1x breadboard

1x stroombron

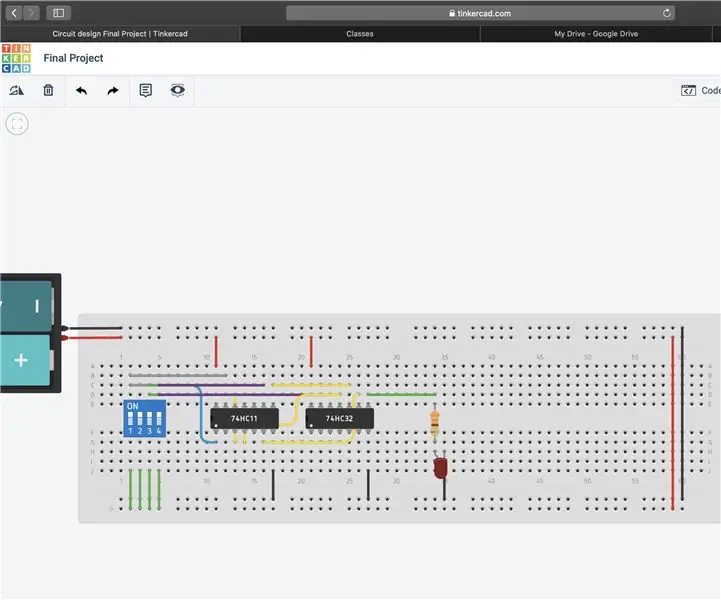
Stap 4: Configureer het circuit

Het laatste deel is twee om het circuit te configureren op basis van de vergelijking. Zie de afbeelding hierboven voor een voorbeeld. Deze schakeling is voor de vergelijking AB(C + D) + ACD